The strong force is technically a theory defined by a quantum field called the gluon field. It is part of the Standard Model of particle physics, which mathematically is a quantum field theory incorporating the fermion field of all matter particles - quarks and electrons, the electroweak boson fields, the gluon field and the Higgs field. In this article we will explore what this quantum field theory is about. It is very difficult to introduce QCD without getting into some technical jargon. There will be a lot of unfamiliar words but I hope to explain why they are there and why they are useful.
QCD, Mathematically Speaking
Wikipedia describes what a quantum field is quite well. For a classical field, a system can be described by a small set of variables; the dynamics of the system is the time evolution of these variables. For a quantum field, the variables are turned into operators (functions over the space of physical states) and the system itself is encoded into a wavefunction, a description of the quantum state of a system of one or more particles. There is a subtle point here: the field itself is not a wavefunction but the equations that govern its time evolution look a lot like wavefunction formulations. Here, unlike in a classical field, there is no variation in strength of the field in different points in spacetime. The variation is instead a difference in something called phase factor, a unit complex number commonly used in quantum physics.
The quantum field theory behind the strong force is described by a surprisingly simple-looking equation, a Lagrangian. The Lagrangian of a dynamical system is the mathematical function that summarizes the dynamics of that system. If you would like a more thorough understanding of the Lagrangian, try this Harvard University physics course (for real enthusiasts or for those who want to go on to a graduate degree).
Although at first it appears reasonably simple, once one begins to explore this Lagrangian in detail, the mathematics involved become very complex and difficult to solve (even for the experts!) and QCD very quickly becomes one of the most difficult theories to understand. There are different versions of QCD (versions of the Lagrangian) that work best for particular problems. For example, lattice QCD examines the thermal behaviour of QCD very well. This is the version physicists use to probe the nature of quark-gluon plasma, where at extremely high energies, quarks and gluons are thought to exist in a free soup-like plasma state, which they believe existed shortly after the Big Bang. A similar physical state, called quark or QCD matter, may be found deep inside intensely dense neutron stars.
What the mathematics of QCD predicts can be tested inside high-energy particle colliders and there is a great deal of research in this field currently going on. Here, as newcomers to QCD, we will focus on how the theory enhances our intuitive understanding of how gluons and quarks interact inside the nucleon.
QCD Is Part of the Gauge Theory Behind the Standard Model
We have explored the proton in recent articles (for example, look up the subheading "The 1/2 Spin of Protons and Neutrons is a Mystery" in the last article, Why Do Particles Have Spin?). Over the last 30 years our concept of the proton has become much more complex than the simple picture of three quarks and a number of binding gluons interacting together to form a little sphere. Today it "looks" more like a seething fuzzy-edged ball filled to brim not only by three quarks but with many more gluons than first thought and possibly with virtual quark-antiquark pairs as well. This new picture comes from many recent high-energy collision studies where protons are smashed into protons at almost the speed of light. As collider velocity (energy) increases, so do the numbers of particles created, offering an increasingly detailed picture of what is going on inside protons.
QCD, in addition to being a quantum field theory, is a gauge theory. Gauge theory is an important part of quantum field theory. It forms the basis for the Standard Model of particles. These particles are shown below.
 |
| (MissMJ;Wikipedia) |
From this symmetry group (called a Lie group) you get a vector field (the assignment of a vector to each point in spacetime), and when you quantize this vector field you come up with a quantum of each gauge field and this quantum is a gauge boson particle, something you are probably familiar with by now. Photons, W and Z bosons and gluons are all gauge bosons. These gauge field theories describe the dynamics of particles, how they act and interact with each other. QCD is a gauge theory with the symmetry group SU(3) (special unitary transformation on complex 3D vectors). It describes the strong field and its eight associated bosons called gluons.
In this article we will explore how quarks and gluons interact with one another (QCD) by comparing QCD to its closely related and much simpler analogue theory - quantum electrodynamics, or QED. QED may seem familiar to you if you have read past articles, as I have talked about it several times. Like QCD, QED is one of quantum field theory's most important foundation theories. It is a gauge theory with the symmetry group SU(1), the simplest possible transformation of the gauge at a point in spacetime, which transforms via its use of complex numbers. It has one gauge field, the electromagnetic field, and one gauge boson, the photon. To get our bearings, the Standard Model is a gauge theory with the symmetry group U(1) x SU(2) x SU(3). SU(2) is the symmetry group for the weak force or electroweak field and it is associated W and Z gauge bosons.
In 1926, Paul Dirac laid down the foundation for QED with a relativistic quantum theory describing the motion and spin of electrons. The theory was refined in the 1940's by Richard Feynman and others. The basic idea is that electrically charged electrons interact by emitting and absorbing virtual photons, the boson carriers of the electromagnetic force. These virtual photons cannot be isolated or observed but (non-virtual) photons can be emitted in a free state in which they can be observed (the photons of EM radiation). QCD began its development in the 1950's and 1960's with the advent of bubble and spark chambers and the plethora of new particles called hadrons (composite particles made up of quarks) that showed up in them. QCD theory was formulated as an analogy to the earlier QED theory. QCD had to incorporate not just one kind of charge but three (the colour charges). Here, quarks interact through the exchange of boson strong force carriers called gluons. Unlike photons and electrons, gluons and quarks are never observed in a free state with the exception of theorized quark-gluon plasma. These differences from QED make QCD more complex and much more difficult to solve, but the similarities between them can help us to define QCD in terms of how it is structured, and we can't really appreciate the beauty of QCD without looking at this theory's mathematical structure.
Comparing QCD With QED
First, A Look at the Lagrangian
As just mentioned, the dynamics of quarks and gluons can be described by just one fairly simple (in the world of theoretical physics at least!) formula, the Lagrangian, shown below left.
(this and other formulae you see in this article are screenshots taken from the relevant Wikipedia articles)
This is just to show you what it looks like in its simplest form. It is described in more detail in both the Wikipedia QCD article here as wells as in physicist Frank Wilczek's article called QCD Made Simple, which is a great reference for QCD beginners and I highly recommend it. The Lagrangian contains a symbol G (shows up twice in the Lagrangian). This represents the gluon field strength tensor. This is a second order tensor field that describes the gluon interaction between quarks and it is analogous to the electromagnetic field strength tensor F in the QED Lagrangian shown below (you can see a structural similarity between the two formulas),
This field tensor describes the electromagnetic field of a system. Both of these field strength tensors are four-dimensional mathematical objects (they are formulated in special relativity) that can describe a field (the gluon field in QCD or the electromagnetic field in QED) of any physical system with great precision.
Quarks/Gluons Versus Electrons/Photons
In a sense, QCD is an expanded version of the earlier QED theory. In QED there is just one kind of charge - the electrical charge of electrons; in QCD there are three kinds of colour charge in addition to electrical charge. Evidence for colour charge comes from electron-positron annihilation experiments; the design is well described at Hyperphysics. These colour charges are called red, green and blue but they have nothing to do with physical colours. They are analogous to electrical charge in several ways. Like electrical charge, they are conserved. In QED, the massless spin-1 photon responds to electrical charge. In QCD, massless spin-1 gluons respond to colour charge. Whereas the electron, a spin 1/2 fermion, carries electrical charge, the quark, also a spin 1/2 fermion, carries colour charge (we will explore additional comparisons between gluons and photons later on in this article).
In QED, the quark's analogue is the electron. Quark dynamics, however, are a bit more complicated than electron dynamics. Quarks come in six possible flavours - up, down, strange, charm, top and bottom. These six flavours are grouped into three generations.
First generation quarks are up and down quarks. These have the lowest mass and they are the only stable quarks, the only flavours of quark found in atomic matter in other words. All flavours of quarks are perfectly symmetrical with respect to colour charge. This means you can have any flavour of quark with any one of the three colour charges. This symmetry is described by the Lie group SU(3) in the Lagangian and it is part of the gauge group that the Standard Model is built upon. The electron in a similar fashion is one of six possible lepton flavours - electron, electron neutrino, muon, muon neutrino, tau and tau neutrino. These six flavours also happen to be organized into three generations. The lowest mass electron and all the neutrino flavours are stable but only the electron is a part of atomic matter.
Adding bosons, particles of force, to our list of quarks and leptons we have the following table (below left) useful for reference (this includes only the stable quarks and leptons as well as their antiparticles):
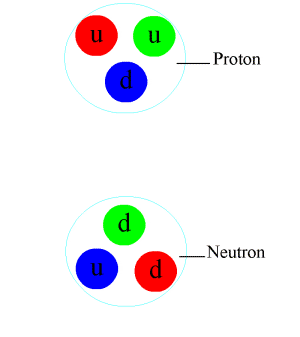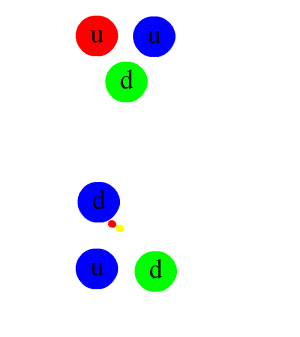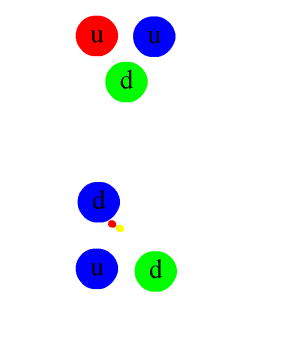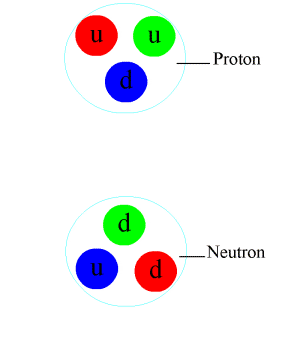
Unlike an electron's single e- charge, a quark can carry a single unit of any of three possible colour charges IN ADDITION TO an electrical charge. More specifically, quarks carry fractional electrical charge. Up, charm and top quarks have a +2/3 electrical charge, whereas down, strange and bottom quarks have a -1/3 electrical charge. This is why a proton (UUD) has a +1 electrical charge and a neutron (UDD) has no charge.
QCD Coupling Constant Versus QED Coupling Constant
The strong force, as mentioned, is much stronger than any other fundamental force. It is only effective up to a distance of about 10-15 m, but it is 137 times stronger than electromagnetism, the next strongest force. Gluons respond to the colour charge of quarks much more vigorously than photons respond to electrical charge. The QCD coupling constant in other words, is much stronger than the QED coupling constant. The Lagrangian of either theory has two general parts - an interaction part and a kinetic part. The coupling constant determines the strength of the interaction part. As we will see later on, knowing the relative strength of different coupling constants gives you a good idea of how the dynamics of a system will play out in reality (a hint: quarks have both electric and colour charge, but they have very different coupling constants - how do these forces play out inside a proton or neutron?)
In particle physics, where high-energy colliders are used, you may hear the term QCD scale to describe mass-energy. It is around 200 MeV. Above this energy density, quarks and gluons are thought to exist as separate components (free particles) in quark-gluon plasma (QGP). Below this energy, they are confined inside hadrons. This is the energy at which QCD coupling gives way. The temperature at which quark gluon plasma is thought to exist, 2 x 1012 K, corresponds to the kinetic energy of about 200 MeV per particle. Colliding two large nuclei together (at CERN SPS (http://home.web.cern.ch/about/accelerators/super-proton-synchrotron) (lead nuclei) and BNL RHIC (gold nuclei) colliders) can achieve this energy, and there is evidence that droplets of QGP have been created in such "fireball" collision events.
A neutron star is much cooler than 1012 K, but its core is so dense that quark matter may exist there. At around 400 MeV of chemical potential energy, hadrons are squeezed together so tightly that they should melt into a quark liquid (rather than the plasma state described above).
The strength of coupling changes depending on the energy of the system. This is where QED and QCD show remarkable and interesting differences. In QED, according to perturbative theory, the beta function is positive. Perturbation is a set of mathematical approximation schemes that allow you to study a very complicated system based on your knowledge of a simpler one. A subfield of QCD is perturbative QCD. These approximation techniques can be used in high-energy cases where the strong force coupling constant is small. It is limited in scope but absolutely essential to make testable predictions of QCD possible because under most circumstances QCD is almost impossible to solve mathematically.
A QED positive beta function tells us that as energy increases, the coupling becomes stronger - photons respond much more strongly to electrical charge at high energy. Quark coupling is different in two important ways. First, the coupling strength DECREASES logrhythmically as energy increases. This is a phenomenon known as asymptotic freedom, which means coupling increases with decreasing energy. In atoms at everyday temperatures, quarks and gluons are very tightly bound inside the nucleus but at very high temperatures (high energy) quarks and gluons are only very loosely bound and transition into a quark-gluon plasma instead.
The second difference is something called confinement. In QED, the attractive force between (virtual) photons decreases with distance. Think of pulling two play magnets apart. It gets very easy as soon as you have a few millimetres of distance between them. In QCD the attractive force between gluons does not decrease with distance. This is also very different from the electric field of charges such as electrons in the atom. The electric field extends into space and weakens with distance. This means that electrons furthest away from the nucleus experience less attraction than those closer to the nucleus. These outermost electrons are freer to interact electrically with other electrons to create chemical bonds and they can leave the atom altogether creating an ion. Quarks are tightly confined inside the proton or neutron.
The Strong Coupling Constant Means Jets In Collider Experiments
When a quark-antiquark pair is produced in a high-energy situation and it then separates, the gluon field is believed to form a narrow tube of colour field between them, much like an elastic band. The strong force remains constant so eventually, as the tube narrows, it becomes thermodynamically favourable for the tube to snap and when it does a brand new quark/antiquark pair appears in its place. This means that you can never pull a quark off of a proton or neutron and study it as a free particle. One quark just leaves and a new one pops up instantly in its place because the strong force has enough energy to make a replacement.
When quarks do become separated from a nucleon or when new quarks are formed, as happens in high-energy particle colliders, physicists see jets, narrow cones in other words, of mesons (a quark/antiquark pair) and baryons (particles containing three quarks) rather than free new quarks. No free quarks have been found in any collider.
Below is a Fermilab image, showing the production and decay of a top quark and antiquark (CDF top quark event), after a proton and antiproton are smashed together. The top quark and anti-top quark live too briefly to be seen, but they show themselves by their decays into jets of other particles (green and yellow lines) and two weak force W boson particles. One W boson decays to a positron (light magenta block, lower left) and an unseen neutrino (red arrow, bottom); the other W boson turns into two mesons (part of the spray, right).
The easy part of this kind of experimentation is that mass-energy going in always equals mass-energy coming out. Here, we have two proton masses going in at extremely high velocity. Remember that the proton is about 100 times more massive than its constituent quarks - gluons are massless - because the strong force contributes significant mass-energy. What comes out is the most massive particle/antiparticle pair known; the pair is about 70,000 time more massive (about 173 GeV x 2) than either up or down quarks (1.7 to 5.8 MeV each x 6). But we don't see the top quark because it has a life span of about 5 x 10-25 seconds. Interestingly this is not enough time for the top quark to decay into hadrons as other quarks do. Instead, it decays through the weak interaction producing W bosons and other particles. The complex-looking image above is the closest physicists have come to a "portrait" of this super-massive particle (has about the same mass as an atom of tungsten!). The top quark was predicted to exist in 1973 but was not discovered until 1995 with the CDF experiment at Fermilab.
Wilson Loop: Why Quark/antiquark Mesons Can Exist
You might wonder why mesons (quark/antiquark pairs) don't always instantaneously annihilate when they are formed (note: they are also unstable and quickly decay anyway). The answer has to do with something called a Wilson loop. This is the path in spacetime traced by such a pair created at one point and annihilated at another point. In a confining theory such as QCD, the loop action is proportional to its area, so the area is proportional to the separation of the quark and antiquark. This loop action therefore suppresses free quarks. In mesons, however, which are quark/antiquark pairs, the Wilson loop contains another loop in the opposite direction, leaving only a small area between the loops, meaning that meson particles are allowed. The Wilson loop creates an excitation of the colour quantum field that is localized on the loop. In QED, Faraday's fluxtubes are analogous excitations of the quantum electromagnetic field.
Deconfinement: A Phase Transition of QCD
Quark-gluon plasma (QGP) is currently only theoretical although there is some indirect evidence it has formed in extremely high-energy collider experiments. For example, RHIC (Relativistic Heavy Ion Collider) released a press release last year (2013) that indicates they may have created tiny droplets of the plasma by smashing gold nuclei together at almost the speed of light. This plasma is also called the deconfining phase of quarks. It consists of asymptotically (weaker coupling as energy increases) free quarks and gluons. Plasma is a state of matter in which charges are screened by a sea of other mobile charges. In the plasmas we encounter on Earth (neon signs are an example), in the Sun and in outer space, it is the electrical charges of ions and free electrons that are screened. In QGP, the colour charges of quarks and gluons are screened.
Lattice QCD Theory Handles Deconfinement
This colour charge is too great to deal with using perturbative computations so it must be dealt with using a different branch of QCD called lattice gauge theory instead. The phase transition from confined quarks and gluons inside hadrons to deconfined quark/gluon plasma is best modelled using lattice QCD, and a number of those models are being tested at both the RHIC and the Large Hadron Collider, two colliders that can collide heavy nuclei together and reach the incredibly high energy density required to deconfine quarks.
One recent formulation of lattice QCD can accurately describe both the masses and the symmetries of the quarks, and using this data, it can predict the critical temperature where the phase transition occurs and it predicts that it is a smooth process rather than an abrupt one. To do this, lattice QCD puts quarks and gluons on a four-dimensional spacetime lattice. Then it turns the problem of summing over all possible quantum configurations of quarks and gluons into a very high dimensional integral that is estimated by using statistical sampling. This method greatly simplifies the daunting number of calculations that would be required (by supercomputers). It describes a smooth transition beginning to take place at around 155 MeV of energy. It can also be used to describe the equation of state of the plasma, and this in turn allows physicists to explore the physical characteristics of it.
Lattice QCD also offers insight into the nature of hadrons. For example, QCD computations show that a meson is not just a paired up quark and antiquark. "Fluxtubes" of gluon fields are also significant components of the meson structure. The image below is from a QCD lattice computation of meson's colour fields (the directions of the flux tubes shown as black lines). It is a computation of a hybrid Wilson loop.
The word fluxtube is borrowed from the analogous magnetic fluxtube of QED, a cylinder of space containing a magnetic field. Sunspots on the Sun are associated with large magnetic fluxtubes, for example, and they form a part of the structure of the Sun's atmosphere.
Chiral Symmetry Breaking: A Challenge For Lattice QCD Theory
There is one drawback to lattice QCD however. It does not account for the chiral symmetry of quarks. Chiral symmetry in QCD is analogous to magnetization in QED. Above a critical temperature, a magnetic material such as iron has no magnetic moment and it is rotationally symmetric. It is demagnetized in other words. Below the critical temperature, however, it spontaneously remagnetizes, and this phase transition breaks its SO(3) rotational symmetry (this is the theory behind why a heated magnet loses its magnetization and then regains it once it cools, although its new magnetic orientation may now be completely different).
It has been shown experimentally that asymptotically free quarks have chiral symmetry. In terms of theory, left-handed and right-handed quarks (this handedness means spin direction relative to the particle's momentum) are treated exactly the same in the QCD Lagrangian when they are asymptotically free. But when they form hadrons (mesons and the baryons of matter), that symmetry is broken (and it can be restored once again at high energy). QCD theory somehow must undergo spontaneous symmetry breaking, in which a symmetrical state ends up in an asymmetrical state. The Lagrangian obeys chiral symmetry but the lowest energy solutions to it must not exhibit this symmetry (the up and down quarks do not come in left-handed/right-handed pairs - they are all left-handed). This is a big bump in the simple elegance of QCD. Solutions to the theory need to take both processes of chiral symmetry-breaking and confinement into account at low energy and it's not easy because these are two very complex phenomena which the simplest form of QCD just can't handle. However, computers are being used to dig into this complex solving procedure, showing good agreement between the expected calculated masses of hadrons coming out of high-energy collisions and their measured values.
No fermions of matter, particles with mass such as quarks and electrons, exhibit chiral symmetry. Massless bosons, however, do (and at high energy the mathematics of QCD describe a "massless quark" that is chirally symmetrical). For a more in depth discussion of this, chiral perturbation theory is discussed in detail here. The process described by spontaneous chiral symmetry breaking is very significant because it accounts for almost all the mass in the universe (excepting the mass contribution of electrons). This process converts very light mass quarks into baryons (protons and neutrons) which are about 100 times more massive, thanks to the contribution of the mass-energy of the strong force. The lattice formulation we were discussing earlier is not compatible with the theoretical process describing chiral symmetry breaking, prompting a number of other versions of lattice QCD, each of which has advantages and disadvantages.
Gluons Versus Photons: Colour Charge
In keeping with the QED - QCD comparison theme of this article, it is especially interesting to see how the photon of QED compares with the gluon of QCD. The photon comes in one type and it is electrically neutral. In general, photons do not interact with each other (with the exception of recent research indicating photon-photon interaction is possible under specific conditions). Under most circumstances, however, a photon going in one direction will go right through another photon going in the opposite direction. I should make the distinction here that photons do not specifically couple with one another but light does interact through higher order processes (interference, superposition etc.)
Photons don't couple because they carry no charge but gluons do carry colour charge just as quarks do. Gluons, in addition to responding to colour charge, can also change one colour charge into another colour charge, and this means that gluons can and do interact with each other. As an example, a blue quark will change into a red quark when it absorbs a specific gluon, which means that the gluon itself must carry colour charge - one unit of red charge and one unit of antiblue charge in this case. Gluons interestingly carry two colour charges consisting of one colour charge and one anticolour charge. A quark, in contrast, can have just one of three possible colour charges. Antiquarks (antimatter twin particles of quarks) can have one of three possible anticolour charges. Incidentally, both the gluons of QCD and the photons of QED (both are spin-1 bosons) are their own antiparticle.
These three colour charges, this additional quantum number in other words, makes otherwise identical quarks in some hadrons (delta baryons possible without violating the Pauli exclusion principle, which states that two or more fermions cannot occupy the same quantum state at the same time.
All three colours mixed together, or a colour and its anticolour opposite, produce white, or a net charge of zero in other words. This means that free particles (protons, neutrons and mesons) always have zero colour charge.
Overall, there are six possible colour charges and eight possible gluon colours.
Why There Are Eight Gluon Colours
Gluon theory describes an octet of gluon colour fields. Each individual gluon has a combination of two colour charges (one of red, green or blue and one of antired, antigreen or antiblue). These two colour charges exist in a superposition of states, which are mathematically given as Gell-Mann matrices. These are an adjunct representation of the SU(3) component of the gauge group, mentioned earlier (the three colour charges of the quarks is the fundamental representation of the gauge group). The Lie algebra, which represents this group has a dimension of eight. Therefore it is a set of eight linearly independent generators, which can be written down as two rows of four below right (these are mathematically equivalent to the eight Gell-Mann matrices).
(The square root of 2 and square root of 6 are required for normalization (a corrective adjustment procedure) of the equations)
Notice how this formulation is entirely of mixed colours. If you could directly measure the colour charge of particular gluon, for example red-antiblue plus blue-antired (that's the top left generator above), the gluon would have a 50% chance of being found as red-antiblue and 50% chance of being found as blue-antired. These eight combos are the only possible combinations of states that are totally independent of one another and independent of the one permitted singlet state (see bottom right above). An additional colourless singlet can also be calculated as part of the matrix, shown below,
(there are actually nine matrices in the calculation) but this last one is forbidden in reality because it would mean that this gluon could exist as a free particle (and give rise to the strong force with infinite range as well).
Below right is an animation of the mechanism of the strong force, showing an exchange of gluons and colour charges.
 |
| (Manishearth;Wikipedia) |
In contrast to the quark, the electrical charge of an electron comes in just one kind. Positive and negative charges are different aspects of the same fundamental electrical charge - they cancel each other out. The question of why some quarks have a fractional positive charge (up, charm and top quarks have a +2/3 charge) and why others have a fractional negative charge (down, strange and bottom quarks have a -1/3 charge) is a mystery, just as why electrons happen to have a -1 charge is. Assigning positive and negative is arbitrary and interchangeable in the theory and the use of fractions is also in a sense arbitrary because it simply balances the atomic charge - you can say the quarks have charges of -1 and +2 and the electron has a charge of -3 instead. This does not answer the underlying mysterious question of why the electron carries more charge than either quark group and why the quark electrical charges come in two strengths and opposite signs. The mechanism of how electrical and colour charges arise in particles is unknown.
Strong Force Between Quarks and Between Nucleons
As mentioned, the strong interaction between quarks is so strong that it has enough energy to produce new particles - a new quark is produced in the place of a quark that is "knocked out" of the nucleon during very high-energy collisions. This force is confined to a scale of about 0.8 fm (10-15 metres), which is the radius of a nucleon, but it does not decrease with distance. This is colour confinement and it prevents the emission of the strong force. Instead of the emission of the strong force, one sees jets of massive particles produced in the collider.
The nuclear force binding protons and neutrons together in a nucleus is also called the residual strong force. This force is thought to be the residuum of the strong interaction between the quarks inside. It is more than powerful enough to overcome the electrostatic repulsion that exists between the positively charged protons in the nucleus. It is this force that is also present as nuclear binding energy and this is what is released during nuclear fission reactions, which are used in nuclear reactors and nuclear bombs. This residual version of the strong force operates under different rules that the strong force between the quarks. It is powerfully attractive at distances of about 1 fm but becomes insignificantly small at distances over 2.5 fm. At distances of less than 0.7 fm, it becomes repulsive, thus it maintains a minimum physical nuclear size.
Field Lines Demonstrate The Meaning of Confinement
In analogy to QCD, electric and magnetic field lines can be drawn just as strong force fields can be drawn. Comparing them offers visual clues to the difference between a confined field and an open field. Below we can see how field lines are drawn for electrical fields. Two repulsive positive charges in close proximity are shown left and two attractive opposite charges are shown right.
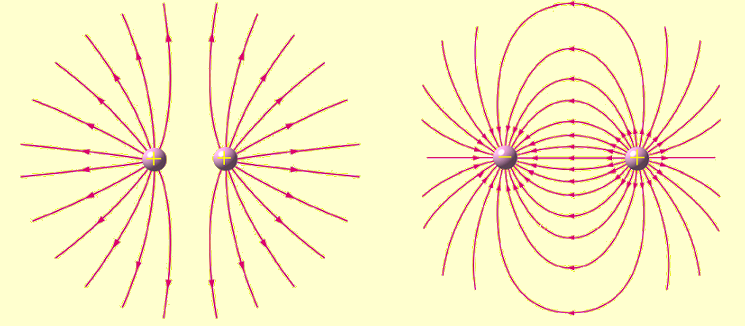 |
| (http://commons.wikimedia.org/wiki/User:Chanchocan;wikipedia) |
The magnetic field lines of a magnet are shown below. Notice how they look essentially the same as those between two attractive charges (above right) because the two magnetic poles are also attractive (attractive force is depicted as field lines connecting the opposite charges/pole). Electrical charge and magnetism are two manifestations of one single fundamental force, electromagnetism, and it deals with all the phenomena associated with QED. In all cases, at least some field lines are shown radiating away from the source of the field. Electromagnetism follows the inverse square law, whereby the intensity of the field is inversely proportional to the square of the distance from the source of the field. This is shown as increasing distance between field lines. In theory, then, the field radiates outward to infinity, though it eventually becomes imperceptibly weak.
 |
| Geek3;Wikipedia |
Like electrical field lines, the strong force between quarks can be drawn as field lines depicting the colour field (see below). A key difference between the two is that while electrical field lines can be drawn radiating away as well as arcing between attractive charges or magnetic poles, colour field lines never radiate away and the arcs are narrowed from one charge to another because they are pulling tightly by gluons (this is not really depicted that well). This confinement of the field confines the quarks within the nucleon.
Below, colour fields are shown for a quark (top center), antiquark (top right; the anticolours are shown as cyan, yellow and mauve) and three mesons (bottom).
.svg.png) |
| Maschen;Wikipedia |
All of these diagrams are two-dimensional out of necessity, but the mathematics behind them actually describes QED and QCD in four-dimensional spacetime. G (in the diagram above) is the gluon field strength tensor, a second order tensor field (geometric mathematical description) that characterizes the gluon interaction between quarks. In QED, an electromagnetic field tensor (F) is used. Classical electromagnetism is described using two three-dimensional vector fields. In QED electromagnetism is brought into one single description that is described in four-dimensional spacetime.
In QCD, the field tensor additionally describes self-interactions between the gluons as well as asymptotic freedom (you don't see that in the simple diagram above). These additional complications of the QCD field tensor make QCD non-linear compared to QED, which is mathematically linear. Unlike a linear system, a non-linear system does not satisfy the superposition principle, which means the output of the nonlinear system is not directly proportional to the input. This makes nonlinear equations much trickier to deal with and is part of why QCD is so difficult to solve compared to QED problems.
QCD, being a quantum theory that encapsulates special relativity like QED, is described on a four-dimensional spacetime framework. In lattice QCD, that framework describes discrete blocks of spacetime whereas in other QCD theories it is described as continuous.
There is a lot of fancy and elegant theory and math here. Yet, quarks and gluons have never been directly observed in any collider. No (massless) gluons or fractionally (electrically) charged particles ever reveal themselves. In a high-energy collider, for example when two gold nuclei are slammed into each other at near light speed, (coloured) quarks and gluons manifest themselves by fragmenting into more quarks and gluons and these immediately hadronize in colourless free particles such as mesons, protons and neutrons. This process shows up as coplanar jets (bunches of particles all travelling in the same direction) in the collider. Most particles in these collisions appear clustered into one of three jets, called a three-jet event. A three-jet event is the most direct physical evidence there is for gluons. Jets are produced when quarks hadronize, and quarks are always produced in pairs (one quark and one antiquark). This explains two of the jets. Some other particle is needed to explain the third jet, and this is theoretically predicted to be a very energetic gluon radiated by one of the quarks. This gluon is so energetic that it hadronizes as well, just like the quarks do. The theory matches up beautifully with experimental observations in colliders.
Conclusion
While QCD is an especially difficult theory to get a grasp of let alone solve, it is also probably one of the most elegant mathematical formulations in theoretical physics, given its simplicity in terms of describing a multitude of very complex phenomena. It is gratifying that this is one theory that can be experimentally tested (high-energy collision experiments) and there is a great deal of indirect verification of the elusive free quark and the gluon, as well as tantalizing work underway to create and to get a good look at mysterious quark-gluon plasma and quark matter, results which are bound to reveal more secrets about what our universe was like just mico-moments after the Big Bang as well as what's going on deep inside stellar beasts like neutron stars.
It is all too clear to me after researching this material that I've only scratched the thinnest surface film of this remarkable theory and I have neglected most of the theories that branch off of basic QCD. There are several different approach strategies for probing QCD further such as continuing to try to solve it with the aid of computer technology, running ever higher-energy collider experiments that can probe deeper into the strong force, and working up various models for QCD in, for example, fewer dimensions or higher dimensions and/or string theory to see if simpler or easier to solve solutions to the Lagrangian are possible. These are just a few possible directions for research that physicists are undertaking. QCD has lots of space for future theorists and experimentalists to try to tweak apart the tightly held mysteries of the strong force.
Next in Quantum Mechanics, try out Why Do Particles Have Spin?











