To keep things as simple as possible I left a few details out of that description of electron-positron annihilation. I will fill you in as we explore antimatter further.
Antimatter is a real mystery to physicists. It is not that they do not know where it comes from or how to create it. The real mystery is where it all went. We will explore that mystery in a little while.
First let me set the scene for you.
Matter is Energy and Energy is Matter
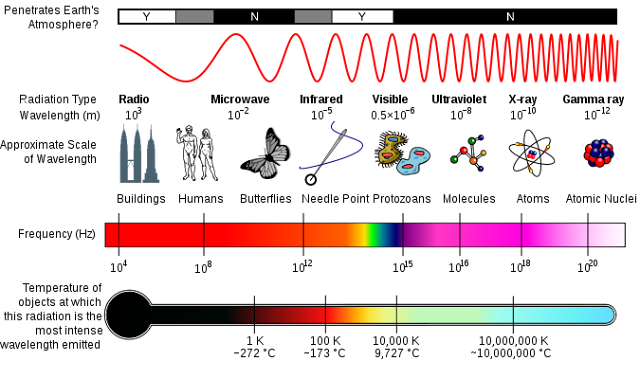
The story begins with Albert Einstein. In 1905, he wrote a now-famous equation E = mc2 or energy equals mass (m) x the speed of light (c) squared. If you think about this, it means that there is a whole lot of energy in even the tiniest bit of mass. A kg of mass (it doesn't matter what kind - it could be an atom-size piece of neutron star matter, filled with squished neutrons, or a cubic meter of air - both contain about 1 kg of mass) equals about 25 billion kWh of energy. To give you an idea of how much energy that is, it could power 100 medium-sized cities for a year! If we could find a way to simply change matter into energy we would solve our energy crisis flat. Wait a minute, we can change matter into energy!
Nuclear fission occurs in a nuclear power plant, and this reaction turns matter into energy. The atomic nucleus of uranium-235 absorbs a free neutron and spontaneously splits into two or more lighter nuclei, shown here:
When this happens, a tiny fraction of total nuclear mass is converted into energy in the form of kinetic energy and high-energy gamma photons.
Mass and Energy Inside an Atom
Atomic nuclei live in a mass-energy equivalent world: If you add up all the mass of the protons and neutrons inside any nucleus you get a sum that is greater than the actual nuclear mass. Why? This is because a force exists inside nuclei holding the protons and neutrons together like glue. It is called the strong nuclear force and it is one of the four fundamental forces in the universe. The mass equivalence of this force, calculated using Einstein's formula, is exactly equal to the difference in mass you get. Big unwieldy uranium-235 nuclei are unstable because they have less binding energy per proton than medium size nuclei - they have just enough to hold the nucleus together, but not forever. Even if never bombarded by a free neutron, each uranium-235 nucleus eventually spontaneously decays into smaller more stable nuclei. This is called radioactive decay and it eventually happens to every unstable element.
Back inside our nuclear plant, kinetic and gamma ray energy is then converted into thermal energy and that heats water to turn a turbine. At the end you get mechanical energy, which is in turn converted into electrical energy.
We are not converting whole atoms into energy here, just a tiny fraction of their atomic mass. And we don't get to use all of that energy either. There is a lot of energy conversion going on between the fission reaction and, let's say, your vacuum cleaner - and usable energy is lost at every conversion step. Additional energy is lost as unusable heat through dissipation and friction along the way, lots of it from transmission lines. Still, nuclear power plants can put out tremendous energy, and they are significantly more efficient that coal, gas or oil energy.
Mass and Energy are Usually Both Conserved
With the exception of nuclear decay, matter and energy are always conserved in all chemical and physical interactions. Let's look at what happens when the bottom of your car door rusts.
The useful conservation rule I just mentioned tells us that every atom of iron in that rusting door is conserved and every atom of oxygen (from the air) is also conserved. Let's see what the reactions involved look like.
It all starts off when 4 electrons (4e-) interact with oxygen in the air. The electrons can come from an electrolyte such as road salt. Road salt doesn't have to be present for your car to rust but it really speeds up the reactions that follow.
O2 + 4 e- + 2 H2O → 4 OH-
Iron, in the presence of water, oxygen and road salt, creates, in essence, a battery.
2Fe(s) → 2Fe2+(aq) + 4e-
Electrons, produced at the "anode end" (Fe(s)) travel to the "cathode end," (O2). The anode end is where an oxidation reaction happens and the cathode end is where a reduction reaction happens. This is an example of how the electromagnetic force is involved in every chemical reaction.
The iron ions and the hydroxide ions then combine to form ferrous hydroxide:
Fe2+(aq) + 2OH-(aq) ==> Fe(OH)2(s)
Ferrous hydroxide oxidizes once again to form ferric hydroxide:
Fe(OH)2(s) =O2=> Fe(OH)3(s)
This compound then dehydrates into rust:
Fe(OH)3(s) =dehydrates=> Fe2O3.nH2O(s) or rust
The "n" means that you can get different kinds of rust, depending on how many water molecules are attached to each ferric oxide molecule.
As complex as the rusting process might seem, it involves only the transfer of matter and energy. No matter or energy is lost or created.
Mass-Energy is Always Conserved
When we talked about nuclear decay, matter and energy were not conserved. Matter was destroyed and energy was created. However, even nuclear reactions must follow the rules of the universe. One very important rule is that total mass-energy is conserved. This means that even in nuclear reactions the total amount of mass-energy remains the same. This rule extends to the universe itself, and it has been instrumental in helping physicists work out how much total energy and mass exist. It also means that the universe, from its first instant, contained all the mass-energy it would ever have and that amount has remained constant to this day.
We've seen how energy can be created from matter. But do we know how to create matter from energy?
The answer is yes but only in very small amounts. Einstein tells us that E = mc2. "c2" is an enormous value, 300,000 km/s x 300,000 km/s. That gives us a clue to the enormous amount of energy we would need to create matter. That is one practical hurdle. The other hurdle is that we can't just order up whatever matter we want, like using a Star Trek replicator. So, let's say we've used a particle accelerator like the one at CERN to accelerate a proton almost to light speed, and we aim it at a small bit of matter. This collision will supply enough energy, in the form of high-energy photons, to break what is called the pair production threshold. The energy, in this case exceeding twice the rest energy of an electron (2 x mec2), will spontaneously create an electron and its antimatter twin, a positron. You can't make just electrons or protons, etc. You can only make matter/antimatter pairs of particles. Positrons, by the way, are much easier to make than anti-protons or anti-neutrons because electrons have a much lower rest mass, and therefore, a much lower energy hurtle to overcome to make them.
Harnessing the Positron
To make positrons, you can use a high-powered laser to drive electrons into gold nuclei. If the electrons and positrons you make have enough energy, they can undergo scattering with more nuclei, radiate more photons, and make more positrons and electrons (another rule of the universe is that charge is always conserved). You can separate the positrons out using magnets and then store them in a positron trap, shown here:
Credit: ARC Centre of Excellence for Antimatter-Matter Studies
This is a vacuum tube with strong magnetic and electric fields that hold positrons in the middle so they can't contact the sides and annihilate themselves with electrons. You can keep a few million positrons at a time with this device.
Positrons are an Important Part of Nuclear Medicine
Luckily you don't need the above procedure to carry out positron emission tomography (PET) scans. This is what a PET scanner looks like:
This scan is used to produce a three-dimensional picture of the metabolic processes going on inside the body. Among other applications, it is often used to detect cancer tumours. First a patient drinks a tracer, in this case radioactive fluorine bound to glucose. Here, all you need is a very small emission of positrons and they come from the positive beta decay of the fluorine. Fluorine-18 decays very fast and it is not very damaging to healthy tissue. The tracer becomes more concentrated in more metabolically active tissues, and cancer cells are very active. Active cells take up the tracer from the blood stream and from there each positron travels for a short distance (less than 1 mm) through tissue, losing kinetic energy and slowing down until it finally interacts with an electron. When this happens, a pair of annihilation gamma photons are created, and they move in opposite directions. They are detected on a scanning device and this device can use the information to localize a tumour.
It takes a tremendous amount of energy to make even small antiparticles such as positrons. And yet, strangely enough, these particles show up spontaneously all the time all around us. Even light reflecting from a mirror creates the occasional electron-positron pair. We call these virtual particles.
Virtual Particles
Virtual particles exist for a very limited time in a very limited space. They must follow most of the same physics laws as real particles do. But they may not exhibit all of the same phenomena. I will give you an example shortly.
Positrons, and in fact all subatomic particles, spontaneously appear and disappear all the time. As I mentioned in my article about light, quantum uncertainty (a probability function) becomes significant over very small distances, such as the inside of an atom. For individual particles, every quality, from mass to speed to momentum, has a range of possible values. Only when we average those values over many many particles do we get results that agree with classical physics.
Real Particle Annihilation
Remember when I talked about spontaneous photon annihilation in the article on light behaviour? Both the electron and the positron which were created from that are virtual particles. Keep this in mind as we continue.
Here I have a Feynman diagram of positron-electron annihilation. An electron and a positron are annihilated and two gamma photons are created:
Notice that I said two photons are created, not one. Are you wondering why, when I talked about light behavior, I implied that this annihilation event created only one photon? This annihilation process, like everything in physics, must satisfy conservation laws, right? Charge is conserved - the net charge before and after is zero in this case. Angular momentum is also conserved. Linear momentum and energy are conserved. Wait a minute here, what about the single photon case?! Doesn't this last law forbid the creation of a single photon? Well it does, for real particles, and this is exactly what happens inside an accelerator like the one at CERN. Real particles at tremendous energies are smashing into other real particles and real particles come out. This is also why we get two gamma rays, each one going off in opposite directions, when we do PET scans.
Side Note About Energies
In the electron-positron annihilation process I've shown here, what you get out at the end depends on how fast you slam the electron and positron together. At the minimum energy to produce annihilation, you get two high-energy photons called gamma rays. These are the squiggly lines labeled γ shown above. At higher energies you can get bigger heavier particles with exotic names like D-mesons, Z-bosons and neutrinos. We will talk more about the Z boson soon but for now, I'll just tell you some cool things about it. It is a force mediator particle just as photons are. However, the Z-boson mediates (carries out) the weak force. This is the fundamental force involved in radioactivity (nuclear decay). Like photons it has no charge but unlike photons, which have no mass, this is a real heavyweight, almost 100 times more massive than protons! Remember that to create any new particle from annihilation you must supply enough energy to match their rest-mass energy equivalent. Z-bosons are massive and that means there's a lot of energy bound up in them that you have to supply.
Let's get back to our comparison between real and virtual particles.
Virtual Particle Annihilation
So far, we have learned that for real particles several conservation laws must be followed. When I was talking about positrons in my article on light, I kept saying that one photon came out of each annihilation event and vice versa. I did not catch myself in a screw-up; this is quite accurate. So what gives? Well, quantum field theory does. The electrons and positrons I was talking about in that article are virtual particles. They don't always have to follow all the same rules. Remember when I said that electrons are held in place away from nuclei inside atoms because of continuous photon exchanges going on between them? A process similar to photon exchange holds the neutrons and protons together inside the nuclei of atoms. In this case, gluons do the job of photons. Gluons are particles that mediate the fundamental strong force.
Side Note About QED versus QCD
The study of gluons and quarks is called quantum chromodynamics, QCD. Unlike the electrically neutral photons of QED, quantum electrodynamics, these particles have different kinds of charge (called colors). This makes the calculations involved even more complicated than the ones for QED (Feynman diagrams are simplified illustrations of this math and they are useful in both theories).
Back to Our Comparison
Gluons are in the same particle family as the Z-bosons I mentioned earlier. For our purposes, the gluon exchange is analogous to the photon exchange. Here's what a Feynman diagram looks like for gluon radiation.
Credit: Joel Holdsworth
Only a single gluon is created, not two. This does not violate linear momentum and energy and this is why: All the particles here are virtual particles. According to quantum theory these particles cannot be isolated or captured. They do not exist as particles! What they are are momentary ripples or excitations within fields, in our case, the strong nuclear force field. We no longer need all the rules for the motion of classical objects, but we do need some rules. I hoped to blow you away when I said in my light behavior article that particles are moving backward through time right under your nose. I cheated a little: These particles, positrons, are not whizzing around you and banging into things, setting off annihilations and emitting gamma radiation all over the place. They are virtual positrons and they reign only inside the quantum world within and closely around atoms. You are safe around reflecting surfaces! However, virtual particles can and do impact our everyday world around us, and if you were reading my last article carefully, you already know this. I have more 'proofs' to share with you shortly. And I promise to revisit this crazy backward time notion, both in this article and in more detail in a new article coming up.
Quantum Foam
Physics on the tiny scale of the atom occurs within an environment called quantum foam. It is on this scale where antiparticles show up and, just as quickly, disappear. Even tiny wormholes and black holes pop in and out of existence. This scale is called Planck length - it is unimaginably short, 1.61 x 10-35 m. The strange things that go on here occur over instants of time as brief as 5.39 x 10-44 s (Planck time). We are now at the extreme limits of space-time. Distance and time cannot be cut into shorter pieces, not even theoretically. On a larger scale, space-time appears smooth but that appearance breaks down at the Planck scale. We don't have a theory of quantum gravity yet so we don't have a complete picture of what space-time actually looks like at this scale, but for our purposes the term, quantum foam, works just fine.
Energy curves space-time*, so at Planck scale, energy fluctuations are large enough to make it choppy or foamy. Here, virtual particles poof into and out of existence. These virtual particles are themselves space-time! That means that they can and do show up as fluctuations within even perfectly empty vacuums, and these fluctuations mean that vacuums have energy. Physicists don't yet know for sure how much energy this is, but out of necessity pairs of virtual particles cannot pop into existence unless they have 2mparticlec2 energy. This extreme energy, called vacuum energy, also makes tiny wormholes and black holes possible. This is a strange concept: space-time's tiniest components are filled choc-a-block with energy. We are soaked in this energy right now, and yet it is not available to us, for example, to do work. Oh wait a minute, it is!
* Einstein defines energy more specifically as energy-momentum in his theory of general relativity. You might have heard that very massive objects (big stars, black holes) warp space-time. Any mass, even an atom, warps it a little. Recalling that mass and energy are equivalent (right?), we can say that anything with energy, mass or both (momentum) will bend space-time. This means that even photons should be able to generate gravitational fields. There is still some speculation that they can't. Photons have what we call relativistic mass (they are massless but have energy, and they also have a kind of momentum called angular momentum). Electrons and quarks (stuff inside matter) on the other hand have rest mass (we experience them as having mass). Here, again, we find ourselves trying to mix quantum mechanics (electromagnetic field propagation) with general relativity (the bending of space-time, or gravity). And no matter how many ways we keep knocking at that door it just won't budge (yet).
Virtual Particle Behaviours
I invite you to take a look at a phenomenon called the Casimir effect. Wikipedia explains it well for us. Here, virtual photons exert a significant and measurable force on two parallel metal plates. Virtual particles also mediate the static electric force between charges (mediated by photons), magnetic fields (again, photons), the near fields of radio antennas (photons), the strong nuclear force inside atomic nuclei (gluons), the weak force (W and Z bosons) and the list goes on. Virtual particles bubbling in and out of existence create much of the phenomena we see all the time. They don't create all of it. The electromagnetic force is mediated by real photons, and virtual ones, as we will see right now.
Real versus Virtual Particle Behaviour - Near Fields
Remember the near field I just mentioned? At a distance of up to about 1 emission wavelength from an antenna, a special kind of electromagnetic force operates. It is mediated by virtual photons, which create strong inductive and capacitive effects from the current and charge within the antenna. What really sets it apart from the 'real' electromagnetic radiation coming from the antenna, called far-field radiation, is that near-field radiation decreases in power far faster. Depending on how far you are away from the antenna you see the effects or one or the other of the two different "kinds" of electromagnetic (EM) radiation, one mediated by virtual photons and the other mediated by real photons. Virtual photon-mediated near field radiation exhibits some very strange behavior. 'Real' EM radiation consists of an electric field component (E) and a magnetic field component (B), where the values E and B are equal at any point in space. You will see this if you refer back to the first diagram in my last article, "The Behaviour of Light." 'Real' EM radiation is an example of a transverse wave. It can be polarized perpendicular to the direction of travel in one, and only one, of four different ways. Virtual EM radiation behaves differently. First of all, the relationship between E and B is very complex and E doesn't have to equal B at all. Second, it can exhibit all four kinds of polarization simultaneously. I'm not sure if anyone knows exactly how near field EM radiation works but it has a great many practical applications such as wireless communication between smart phones and tablets. For example, soon you will be able to buy an Apple iPhone with an NFC (near field communication) chip in it. You input your credit card information and simply place your smart phone near a store's reader to purchase your items. I'm not sure how they worked out the security on that.
Some Particles Are Their Own Antiparticle
Every virtual particle pops into existence with its own antiparticle. You might be wondering how the virtual photon/antiphoton pairs interact within the strange virtual electromagnetic field I mentioned above. The answer is bit disappointing: some particles are their own antiparticles. Most of them are force carriers and they include photons, Z bosons (mediating the weak nuclear force) and gluons (mediating the strong nuclear force). All antiparticle twins of particles bear opposite charges. Positrons, electron's antimatter twins, are positively charged for example. However, particles that are their own antiparticles, must all, as a rule, be electrically neutral.
Where's the Antimatter?
We now know that antiparticles (recall that subatomic particles make up matter and force) represent one side of the virtual particle pairs that make up quantum, or Planck-sized, spacetime. After some thought, this begs some very fundamental questions. If particle/antiparticle pairs are created everywhere all the time, then why isn't the universe made up of half of each kind? Why is there any matter at all, when every pair that is created almost instantly annihilates itself? To answer these questions we will have to equip ourselves with some pretty challenging theoretical background. We will be exploring some theories still in progress beyond this point, and theories might change a little or a lot over the next few years. Let's give it a try. (If the following symmetry theory is too confusing, please skip to my Brief Conclusion below. I think you will enjoy the two movies I have included. I found the symmetry theory very challenging and would greatly appreciate any corrective feedback from experts.)
Symmetries Were Broken When the Universe Began
When the universe first exploded into existence it contained nothing but energy and a lot of it. This energy was, at first, homogenous. It was all the same everywhere. Each of the four fundamental forces rapidly settled out of this primal force, one after another, each through a process called symmetry-breaking. All this happened in less than 10-12 second. The process of symmetry-breaking operates much like a phase transition does. Examine a glass of water right at the freezing point. The water is undergoing a phase transition. Water in one phase, ice, settles out of water in another phase, liquid. You can see the separation quite easily and in our application we will call this separation the domain wall. It is difficult to understand how an initially homogenous system, the just-formed universe for example, can evolve into an asymmetrical system when all the forces acting on it should be acting symmetrically. However, much like how ice formation breaks the homogeneity of water (it breaks its symmetry), one phase transition that took place when the universe was just forming may be responsible for creating a surplus of particles over antiparticles. This particular kind of phase transition allowed the electroweak force to settle out. When it settled out, a special kind of symmetry called P-symmetry (you can think of it as the symmetry of the three coordinates of space, called parity was broken. This meant that another kind of symmetry called C (charge conjugation) symmetry could also be broken. Electromagnetism, gravity and the strong force have already settled out at this point. They settled out when C-symmetry was still intact so these fundamental forces all observe this symmetry. The weak force, however, settled out from the electroweak force just after C symmetry was broken so it does not observe it.
Example: The Weak Force Violates CP Symmetry
Nuclear decay is mediated through the weak force. The weak force only acts on left-handed particles, and right-handed antiparticles. The direction of spin and the direction of motion are opposite each other in left-handed particles and in the same direction in right-handed particles, as shown in the diagram below. Any particle can be either right or left-handed.
Broken Symmetry May Explain Why Our Universe is Made of Matter
Quarks, Antiquarks and Matter
First of all, let me introduce you to the quark. This particle is a fundamental constituent of matter. Quarks combine to make composite particles called hadrons, two of which are stable and these are the protons and neutrons inside an atom's nucleus. Another result of the CP symmetry-breaking we talked about earlier, is that some probability amplitudes for quarks are not equal to the corresponding amplitudes for antiquarks. By themselves these differences mean that quarks do not observe CP symmetry and yet we know that they do. Let me explain: Time reversal has its own probability, and when we include time (with its own form of symmetry), a larger symmetry, CPT symmetry, is conserved. This means that as long as antiparticles move backward through time, the universe can theoretically have an exact mirror of itself (called parity (P) conservation), including mirror images of all of its forces and particles. All of our laws in physics point to this mirror-ability.
Antiquarks Are Filtered Out . . .
Getting back to our quarks: Both quarks and antiquarks have the same phase and the same positive energy as they move in space-time. However, their phase depends on their mass. Both have identical mass too, but their mass depends on two variables - flavor and something called the Higgs VEV (an expected value of the energy of a vacuum). What's interesting here is that the Higgs VEV isn't homogenous - it varies along the domain wall. The domain wall is the separation line that is created when symmetry is broken. Because of this, some probabilities for quark qualities differ from the corresponding probabilities for antiquarks. This means that quarks and antiquarks may have different reflection and transmission probabilities through the domain wall. And this (finally, bear with me) means that more quarks coming from the unbroken side are transmitted compared to antiquarks. These quarks are then added to the broken-side quarks, which were already there. These are the new quarks of our universe.
. . . And Removed (well, remade into something else)
In the unbroken phase, something called the sphaleron interaction occurs. Here, in the high-energy environment of the new universe, the sphaleron converts all baryons to anitleptons and antibaryons to leptons. Baryons here include the hadron-making quarks that contribute to matter (protons and neutrons). Leptons are electrons and their relatives. The sphaleron interaction almost never happens under ordinary conditions but in the extreme heat and pressure of the new universe it happened a lot, and what it did was wipe off all the, now excess, antiquark content in the unbroken phase by turning them into leptons such as free electrons, etc. This left an excess of quarks in the universe, an excess of matter over antimatter. The same kind of process happened with all the elementary particles, seeding the universe with particles over antiparticles.
A Brief Conclusion
Our universe is almost completely made of matter because of the way it unfolded. Antimatter really does exist but, under ordinary circumstances, it doesn't exist for long. We need to magnetically separate any antimatter we create and we need to keep it held apart from matter using strong magnetic and electric fields. It will be a long time before we can engineer something like an antimatter rocket that can harness the incredible energy that is released when particles collide with their anti-particle twins, or will it? Take a look at what NASA's been up to. Scientists have been looking into whether a positron-fueled rocket could get us to Mars. This is an artist's conception of what it might look like:
This is a proposed design for an antimatter engine that might work:
It is theoretically possible that a universe could unfold on the "other side" of broken symmetries. Perhaps our universe's theoretical mirror twin does indeed exist somehow somewhere, and in that universe, perhaps an antimatter technician is using EEM (electron emission tomography) to scan her antimatter patient for antimatter tumours, the inner doors of an antimatter car are rusting out to the annoyance of an antimatter me, and antimatter scientists are pondering an exotic-sounding matter-fueled rocket. This 3-minutre video sums up our antimatter story very nicely:
This 24 minute Cosmic Journeys video, which aired in August 2011 explores our current knowledge of antimatter in depth. Here you will find out how scientists are looking for antimatter in our universe. It's high def with great imagery, one of my favourites!
A final note: I explore how the universe became seeded with matter over antimatter in my article "Our Universe Part 8: Hadron Epoch." There you will find a similar but slightly different take on this theoretical process.