Why Dark Matter?
These effects, calculated using Newton's and Einstein's gravity formulas, are off, and that discrepancy has been measured very accurately. Physicists have calculated exactly how much extra matter would be needed to get the observations back into line with the theoretical predictions. These results are shown in the top pie chart below.
A Few Notes On What Matter and Mass Are
The top pie chart represents the total matter and energy content of the current universe. Einstein famously described how matter and energy are equivalent and interchangeable (E = mc2). This is known as mass-energy equivalence. I am using matter and mass interchangeably in this article but I should remind you that I am not being quite accurate. Mass in physics is a much better defined term than matter is. Matter, described as having both mass and volume, is not as useful. For example, the Pauli exclusion principle explains why atoms of matter cannot overlap each other and therefore require space, but this becomes less relevant when we study the ultra-dense matter inside white dwarfs and neutron stars. When we study particles approaching the speed of light, mass also becomes tricky. We must deal with two kinds of mass - rest mass and relativistic mass. This is why in modern physics both mass and matter are better treated as energy-momentum tensors. These tensors describe not only matter at any point in space-time, but also radiation and force fields present (with the exception of gravity) as well.
The Universe's Matter and Energy Content Evolved
As far as anyone knows, the universe is an isolated system. This means that, according to the second law of thermodynamics, its total mass-energy has remained constant since its inception as the Big Bang. In the current universe, dark matter accounts for 26.8% of the total mass-energy of the universe, and over 84% of the universe's total matter. You will notice that most of the mass-energy of the universe is dark energy. Dark energy is even stranger than dark matter. It is a hypothetical form of energy that accounts for the observed acceleration of the expansion of the universe, and it makes up more than 68% of the total mass-energy of the current universe. Dark energy, in itself, acts as a homogenous negative pressure throughout the universe, and will be explored in detail in a future article. For now, let's take a micro-lesson in dark energy:
The lower pie chart describes the mass-energy makeup of the universe when it was very young, about 380,000 years old. It looks very different! There is negligible dark energy. We don't see any because the universe expansion rate did not begin to accelerate until about 5 billion years ago. Before that, the universe expansion rate was actually decelerating because of the attraction of dark matter and baryonic matter to itself and to each other. Baryonic matter is ordinary atomic matter made up of protons and neutrons (baryons). That gravitational attraction is still there in our current universe but it is now overwhelmed by the increasing influence of dark energy.
The simplest explanation for dark energy is that it is the cosmological constant. This means that it is fundamental to the nature of a vacuum, which is what outer space essentially is. A vacuum has intrinsic energy, sometimes called vacuum energy. Physicists know this energy exists because there are several lines of observational evidence for it, for example, the Casimir effect. This energy has negative pressure. Here, things might seem a little counter-intuitive because a vacuum acts differently than a volume of air, for example. If we take a sealed container full of air molecules at a specific temperature and allowed that container to expand, the temperature of the air would drop, according to the ideal gas law, because the total energy (for an ideal gas it is all treated as kinetic energy) of the molecules, which must remain constant, is now distributed over a larger volume. The average kinetic energy (which is the temperature) of the air drops. This is why rising (expanding) warm air cools in the upper atmosphere. In a similar way, what started out as gamma rays from the Big Bang now strike Earth over 13 billion years later as much lower energy microwaves. This process is technically called adiabatic expansion. A vacuum is different. It has an intrinsic fixed amount of energy (potential energy in this case) that depends only on its volume, so that a larger vacuum has more energy and a smaller vacuum has less energy. As the vacuum of the universe expands, the amount of vacuum energy increases, increasing the universe's negative pressure, and accelerating its expansion rate further. How this expansion does not break the second law of thermodynamics (remember that the total mass-energy of the universe should not change) is a mystery to be solved in the coming article.
This is our earliest visible glimpse of the universe, made possible when photons and electrons decoupled from each other. By about 380,000 years old, the universe had expanded and cooled enough so that photons, previously trapped in opaque electron-dense plasma, were able to stream outward in all directions. These photons are still streaming. They are what we detect as cosmic microwave radiation background.
Notice in the lower pie chart that the very young universe contained a significant photon component. Our current universe, in contrast, contains very little electromagnetic radiation or photons, most of it in the form of cosmic background radiation - the faint whisper leftover from the roar of the Big Bang. The early universe was flooded with very high-energy gamma rays. A smaller photon contribution comes from stars as well. Additional radiation from stars today is also much weaker than what once streamed from the first enormous and very brightly burning stars that formed around that time. As you can see in the pie chart, the very young universe actually contained more radiation than matter, so where did it all go? Radiation transformed into matter through a process called pair production. For example, two very high-energy photons (gamma rays,γ) can annihilate, forming a positron and electron, particles of matter. This is how quarks, the particles that make up protons and neutrons, formed as well. The reaction is actually reversible. It favours photon production in very high-energy environments and matter production at lower energy. This simple reaction really shows off how matter and energy are intimately related to each other. At around 380,000 years old, the universe's energy was low enough to favour matter production but high enough that photons had enough energy to transform into the rest mass of various particles.
γ + γ ↔ e-+ e+
According to this formula, matter and antimatter (the positron e+ is an example of antimatter; there are antiquarks as well) should have been produced in equal amounts, but we know that the current universe is dominated by matter. Particles of matter and their antimatter twins immediately annihilate upon contact with each other, so why is there any matter left at all? A slightly imperfect symmetry in the weak force, called CP violation accounts for it, luckily for us. How that works is a subject of another article called Antimatter.
What Dark Matter Does
In the 1930's, physicists discovered that the mass of galaxies calculated from their gravitational effects was far greater than the mass calculated from all the visible matter they contained, things such as stars, gas and dust. They coined the term "dark matter" for this mysterious invisible mass. Since then, more evidence pointing to dark matter has come from cosmology. For example, galaxies rotate much faster than they should, based on their observed luminous material.
This is an interesting problem and you might be surprised that it took so long to come to light. After all, the orbital velocities of planets around our Sun, for example, were worked out in precise detail centuries ago by Johannes Kepler, later incorporated into Newton's laws for classical mechanics. According to these laws, the orbital velocity of a body in a system with mass concentrated at the center, decreases with distance from that center, shown by the blue dotted line, A, in the graph below. A galaxy, though much larger and more massive, should work just the same way, and yet it doesn't. Stars far from the galactic center orbit with the same velocity as those very close to the center of the galaxy, as shown below by the red line, B.
 |
| PhilHibbs;Wikipedia |
This leaves two options: First, there is far more mass than what is visible in the galaxy and this mass must not only envelop the galaxy's visible disc but extend far beyond its edge as well in a spherical halo in order to account for the almost flat velocity line. This allows rotational velocities to fall off far out into the halo, agreeing with Newtonian mechanics. Physicists have been able to map the dark matter halo that surrounds the Milky Way by measuring how dark matter alters the paths of smaller galaxies and star clusters that orbit our galaxy. It looks like a giant squashed beach ball, shown in the brief video below.
The second option is that Newtonian laws, though perfectly adequate for solar-size systems and smaller, do not describe gravitational behaviours of very massive large-scale objects. General relativity, the modern theory of gravitation, incorporates special relativity into Newton's law of universal gravitation, and gives physicists a new four-dimensional metric called space-time. Though this theory revolutionized the concept of gravity because it handles the passage of time in space, the motion of bodies in free fall and the propagation of light, it cannot describe this behaviour either.
A second line of evidence for dark matter comes from the phenomenon of gravitational lensing. Einstein's theory of general relativity predicts that light from a source is bent when it passes through a strong gravitational field. The figure below created by NASA shows how light from a galaxy directly behind a massive object (the gold sphere) is made visible as two twin images seen by Earth.
The orange arrows show two apparent locations for the galaxy. The white arrows show how light is bent from the actual position of the galaxy, around the massive object.
This effect was theoretically put together in the 1930's but it was not confirmed by observation until 1979, when a double image of a distant quasar was discovered. The intervening mass of a large elliptical galaxy between Earth and the quasar bends the light coming from the quasar into two images, shown as A and B in the image below right.
 |
| Matthias Langer; AIR-WKDo Aylin Esen and Ander Hosgar;Wikipedia |
A third line of evidence for dark matter comes from the cosmic microwave background (CMB). Below is an all-sky map of the CMB created from WMAP data.
CMB radiation, discovered in 1964, is a blackbody spectrum. When the universe was about 1 second old, it was a near perfect blackbody in thermal equilibrium, with a temperature of about 1010 K. It had a near perfect ability to emit energy through radiation. In 1992, physicists discovered that it is not the perfect blackbody you would, expect expanding equally in all directions from an initial point-like origin. The spectrum instead contains fluctuations called anisotropies. These anisotropies have been studied in increasing detail since then, and they provide a great deal of information about the composition and evolution of the universe. In general, the anisotropies match what you would expect if tiny thermal variations, coming from quantum variations in a very tiny space, are blown up like a balloon to universe size. The radiation we see is called the surface of last scattering. This is a spherical surface that represents the locations in space where the decoupling of photons from electrons occurred. The anisotropy of the CMB comes in two types - primary anisotropy, which comes from the last scattering surface and before - and secondary anisotropy, which comes from effects that came after last scattering. These effects come from interactions of the photons with hot gases and gravitational potentials, for example. Secondary anisotropy gives physicists tremendous information about the early evolution of the universe. There is evidence here of the dark age and of reionization caused by intense stellar wind from the very first stars, for example.
The structure of the anisotropies comes from two effects - acoustic oscillations and diffusion damping. Diffusion damping acted to reduce anisotropies as photons, still significantly scattered around by other particles in this hot dense plasma, travelled from hot regions of space into cooler regions, dragging along protons and electrons with them. Its effect is governed by the average diffusion length of photons which can be calculated accurately. It's the acoustic oscillations that are of special interest to us here. The plasma of the very early universe was extremely dense. Acoustic oscillations arose from the competition between baryons and photons within it. Photons exerted a pressure that tended to erase anisotropies and baryons (matter) are gravitationally attracted to each other so they tend to collapse into denser patches, increasing anisotropies. These two counteracting forces created a spherical oscillation in the density of the plasma, working exactly the same way as sound waves moving through air do, except that this "sound" wave was made of photons and baryons whereas a sound wave in air is made of air molecules. The oscillations created the CMB's characteristic spectrum peaks, shown below as you scroll down.
The peaks themselves are resonant frequencies of the oscillations of the plasma in the early universe. A lot of information is contained in these peaks. The angular scale of the first one, for example, gives us the curvature of the universe. The ratio of heights between the first peak and the next peak gives us the baryonic matter density of the universe. Below is a graph of this power spectrum (fluctuations in the temperature spectrum of the CMB) in terms of angular scale. Angular scale (also called multiple expansion or multiple moment) is a mathematical function that depends on angles. It gives you information about fields at distant points in relation to a single point source. It allows you to describe an expansion process in a three-dimensional space. You get the data by plotting the spectrum at different angular scales on the sky using ground and balloon data.
This data was gathered from several instruments: WMAP, Acbar, Boomerang, CBI and VSA. The solid line is a theoretical model.
The specific evidence for dark matter comes from the third and later peaks. Describing how this works requires a bit more background information.
Consider the oscillation we talked about. We will put dark matter into that scenario. Gravity pulled both dark matter and baryonic matter into the denser center of the oscillation. This oscillation is quantum-originated, so it was once quantum-sized, but it grew thanks to the rapid expansion of the universe. As it expanded, dark matter and baryonic matter increasingly collapsed into it. The current pattern of galaxy clusters in the universe is thought to be the leftover signature of not just one oscillation or "sound" ripple, but many overlapping ripples, like waves emanating from an object dropped in a pond, except in three dimensions rather than two.
Only baryonic matter was pushed back by photon pressure. (Nonbaryonic) dark matter doesn't interact with electromagnetic radiation so it continued to fall inward and stay inside each oscillation. This inward-outward baryonic dance gives each fluctuation its acoustical ring. The frequency of each oscillation depends on each fluctuation's size. It gives a temperature spectrum fluctuation because the baryonic matter heats up when it falls in and cools off when it is pushed back out, a spectrum signature, which the dark matter doesn't have. To describe how this translates into spectrum peak data, pretend that the universe contained only photons for a moment. After a perturbation reached its maximum compression, they would flow out, red-shifting along with the expanding universe as they went. This means that the gravitational potential would decay away (with the red-shift) and it would allow the temperature perturbation to be much higher than what it is. The third peak would therefore be much higher. Now consider a universe with only baryonic matter and no photons. (Nonrelativistic) matter doesn't red shift so the gravitational potential doesn't red-shift away and the fluctuations and peaks would be much lower than they are. Mass, in other words, reduces the power spectrum peak amplitude.
This peak data gives a measurement of the total nonrelativistic matter of the universe. These peaks in the power spectrum are much lower than they should be based on baryonic matter alone, translating into a mass that must be non-baryonic and must be about five times greater than the baryonic mass of the universe.
This data also offers a picture of the transition from a radiation-dominated universe to a matter-dominated universe, when photons no longer coupled with baryonic matter and they streamed away, relieving the pressure in the system. After decoupling, the only force acting on the baryons was gravity. Baryons, along with dark matter remaining at the center of each oscillation, formed an over-density of matter at both the original anisotropy site and in a spherical shell at a fixed radius away from it, sometimes called the sound horizon.
The baryon-photon dance is now frozen into the CMB, and the signature of dark matter can seen indirectly in this map where small distortions of the CMB reflect regions of dense matter where photons were gravitationally lensed along their long journey since they were decoupled billions of years ago. These distortions can be used to map the underlying distribution of dark matter in space. The evidence for dark matter is that these frozen fluctuations are about five times smaller than what baryonic matter alone can account for. To understand why this extra mass can't be hidden baryonic matter such as dark gas, black holes and faint planets, we need to look at how baryonic matter was created in the universe. The amount of baryonic matter in the universe is tightly restricted by the nature of Big Bang nucleosynthesis. This process of nucleosynthesis is covered in detail in the article How Atoms Are Made, but let's briefly review it here.
The hot plasma of the young universe contained, along with photons, the building block particles of atoms such as protons, neutrons and electrons as well as other (unstable) particles. As the universe expanded and cooled, high-energy photons were able to decouple and stream away in all directions, giving protons and neutrons a chance to stick together and create deuterium nuclei. Eventually, larger nuclei could form such as helium-3, helium-4 and lithium. This is called Big Bang nucleosynthesis. This process slowed down as the universe continued to expand because the density of the plasma decreased, offering fewer collision opportunities. The neutron is unstable by itself, with a lifetime of about 15 minutes. After that, all free neutrons were gone and nucleosynthesis came to a stop altogether. No elements larger than beryllium were formed. This brief window gives a strict maximum on how much baryonic matter could have formed in the universe. All larger atoms subsequently created inside stars and in supernovae were created from this limited supply of smaller atoms. Gravitational evidence for additional matter means that it cannot be baryonic in nature.
What Dark Matter Is: The Hunt For the Dark Matter Particle
The first obvious place physicists looked was for matter that is not easily detectable. It must not be luminous and therefore cannot be observed through a telescope. There are several sources of what is called baryonic dark matter (dark matter made of atoms) out there: non-luminous gas, black holes, neutron stars, white dwarfs, brown dwarfs, very faint stars and planets. These objects are collectively called massive compact halo objects (MACHOS). You might think that ultra-dense black holes alone might be enough to account for the effects of dark matter. There are two main reasons why dark matter can't be them or any other baryonic matter.
MACHOS account for only a very small fraction of baryonic matter, which itself is highly restricted by the calculations of Big Bang nucleosynthesis. As we saw earlier, they put a strict upper limit on the universe's total baryonic mass. Therefore, MACHOS cannot be enough to contribute the massive amount of dark matter. Second, the analysis of the tiny irregularities in the cosmic radiation background described above show that around 85% of the total matter in the universe does not interact with ordinary matter or with photons. It can't be baryonic, in other words.
Most physicists think dark matter must be some kind of nonbaryonic particle with mass and which is not easily detectable, which means it must only very weakly interact with electromagnetic radiation, if at all. There is no verified particle that matches this description except the neutrino. Like photons, neutrinos decoupled from the plasma of the early universe and began to stream freely in all directions. Physicists are looking for a comparable neutrino cosmic background, a much more difficult job since neutrinos interact only with the weak force and gravity. The effort, though, might reap huge dividends because neutrinos decoupled when universe was just two seconds old, offering a far earlier picture of the universe than photons (at 380,000 years) can. What will make these neutrinos even more difficult to detect is that they would be very low energy, unlike more easily detectable high-energy neutrinos streaming from the Sun and from supernovae. Cosmic background neutrinos should be around 1.95 K, whereas the photon cosmic background is about 2.73 K (absolute zero is 0 K). You might think they should be hotter particles since they decoupled from a much more energetic universe than photons did. Photons, neutrinos, electrons and positrons all existed in thermal equilibrium with each other, even after decoupling. What made photons warmer is the electron-positron annihilation that took place afterward (discussed earlier in this article). These annihilations, happening before photons decoupled and creating high-energy gamma rays, transferred energy to the cooler photons in the plasma. This difference in energy remained "frozen" in the two backgrounds ever since.
Neutrinos, like photons, still exist in the present universe. Like photons, neutrinos are stable particles - they didn't decay away - and, unlike photons, they must have at least some mass, a requirement of their flavour oscillation. There should be a large abundance of them in the universe. They hardly interact with baryonic matter and do not interact with photons. All this makes them good dark matter candidates. However, their current contribution (like photons) to the mass-energy of the universe is negligible. Except for neutrinos produced in stars, supernovas, etc., the vast majority possess very little energy. Physicists can also put a strict upper limit on neutrino mass, which means they make up less than 1% of the current mass of the universe. This far too low mass-energy places them out of contention for dark matter. Another problem with neutrinos is that they travel at very near the speed of light. Their near-light speed means that they tend to erase all but the largest scale dark matter fluctuations observed in the universe, rather than contribute to the pockets of denser dark matter where galaxies and galaxy clusters form.
The remaining dark matter candidate particle must be a hypothetical one - an axion or a supersymmetric particle is possible. Supersymmetric particles are explored in the article Supersymmetry. These theoretical particles solve more than one stubborn problem in physics, making them a popular contender for dark matter as well, because the lightest ones should be stable, so they persist in the universe today. The axion is a hypothetical particle that was introduced to solve something called the strong CP problem in physics. As a bonus, like the lightest supersymmetric particles, it is an attractive particle candidate for dark matter. It should have mass and it should be stable. This is how the axion arises: I mentioned CP (charge parity) violation in the weak force earlier. The problem is that the weak interaction should feed into the strong interaction (the force that holds nuclei together) according to quantum chromodynamics theory. This should create a fairly large strong CP violation but no violation at all has been observed. A solution to the problem is to introduce something called the Peccei-Quinn mechanism to the mathematics. This mechanism introduces a new global symmetry to the Standard Model, which is spontaneously broken. This symmetry breaking introduces a new boson particle (the axion) that mathematically fills the role of the large strong CP violating term. If you have recently read Gauge Theory or Supersymmetry, you will certainly notice this technique has a familiar ring to it. By doing so, this relaxes the CP violation parameter to zero, bringing it into agreement with observation. Something called non-trivial QCD vacuum effects (which means that quarks, the building block particles of protons and neutrons, play an important role in shaping the structure of the quantum vacuum) in the mathematics make the symmetry just imperfect enough to impart a mass on the axion, and this is where its potential as a dark matter particle comes in.
Several experiments since the 1980's have been designed to detect the axion cosmologically (in space). These experiments are trying to find what is called the Primakoff effect. According to theory, a strong electromagnetic field should be able to convert axions into photons and vice versa. The Sun's core, for example, should produce lots of axions as X-ray photons scatter off electrons and protons inside powerful electric fields. The CAST experiment is designed to detect these solar axions by converting them back into X-rays using a strong magnetic field. It came online in 2003, but as of 2006 it has not found any evidence for axions. Built in 1983, the Axion Dark Matter Experiment, utilizing the same general concept, likewise has not detected any axions. It is currently undergoing an upgrade to increase its sensitivity. In short, the axion has not been definitively ruled out quite yet but it seems to be on thin ice.
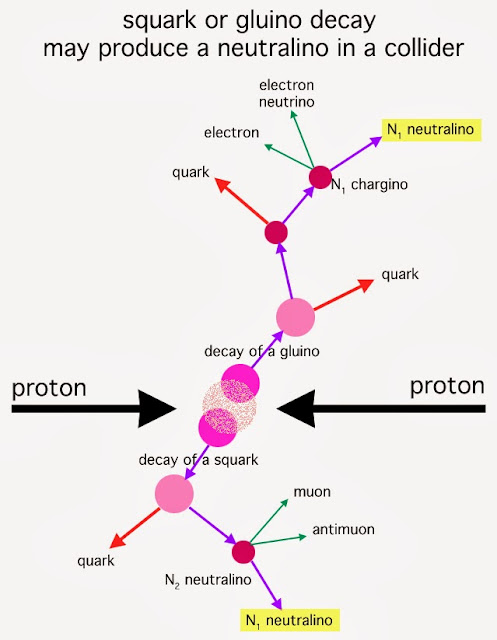
Two other hypothetical candidates come from supersymmetry - the lightest neutralino and the sneutrino, two particles that should have mass and they should be stable. As we saw in the article Supersymmetry, neither of these particles has been detected within their expected mass range inside supercolliders, putting them too on thin ice. However, the LHC is currently being upgraded to achieve enough energy that should either prove or disprove their existence.
Hot, Warm and Cold Dark Matter
You may have seen these dark matter classifications before. They are losing relevance in current physics. All of the nonbaryonic dark matter particle candidates can be classified as either cold, warm or hot dark matter. Hot dark matter consists of particles that were moving close to light speed, such as neutrinos, when clumps of matter that would form galaxies and galaxy clusters began to form. Cold dark matter consists of particles that were moving much slower than light speed at the time of galaxy formation. Warm dark matter is made of particles with intermediate velocities. Hot dark matter now seems unlikely because any clumps that were galaxy size and smaller would have been quickly dispersed by these whizzing dark matter particles. As mentioned earlier, neutrinos were and are in abundance in the universe, and they did and do have these dispersal effects, but they have too little mass-energy to contribute to dark matter. If they had enough mass-energy to contribute to dark matter, only clouds with the mass of thousands of galaxies would have stood a chance. This would have significantly delayed the formation of the galaxies we see today or perhaps even prevented them altogether. Cold dark matter particles, on the other hand, could form galaxy-sized and smaller clouds, allowing galaxies to form first, followed by galaxy clusters as galaxies later merge. Chandra observations support this order of galaxy cluster formation, rather than fragmentation, which would have had to occur with hot dark matter, suggesting that cold dark matter is the only realistic scenario. Cold dark matter particles are MACHOS, and hypothetical particles such as axions, neutralinos and sneutrinos, all particles with mass that travel significantly below light speed.
What If Dark Matter Isn't Matter at All?
No particle clearly stands out as a dark matter candidate, and the window of possibility for detecting them is closing in as experiments become more and more sensitive and powerful. And yet something either interacts with gravity or skews its effects on very large-scale structures. It seems increasingly reasonable to consider that gravity itself may hold the answers. The article Gravity compares Newtonian gravity with Einstein's theory of general relativity if you would like to review them first. Many physicists are reluctant to consider this option because general relativity works so beautifully, aligning observation with theory for almost every phenomenon in physics, except the ones described here.
We would have to consider current theories for gravity as incomplete and, despite the utility of general relativity, there is much food for thought to suggest that it isn't the whole story. For example, gravity does not fit nicely next to the other fundamental forces because it is many scales weaker than they are, and it does not fit into the Standard Model at all - it has no place in quantum mechanics. There is no gauge particle or gauge theory that seems to work for it. Einstein's theory of general relativity describes gravity extremely well as long as physicists are dealing with situations larger scale than an atom - and, possibly, smaller scale than a galaxy.
The first attempt to modify gravity in order to fit galactic rotational velocities was Mordehai Milgrom's Modified Newtonian Dynamics, or MOND, in 1983. This (non-relativistic) model creates a stronger gravitational field when gravitational acceleration levels are low, such as near the edge of a galaxy, but it does not explain gravitational lensing, a phenomenon explained by general relativity. Since then, several attempts have been made to bring general relativity into MOND, such as tensor-vector-scalar gravity (TeVeS) and scalar-tensor-vector gravity (MOG). If you are unfamiliar with scalars, vectors and tensors, they are explored in detail in the Gauge Theory article. It makes sense to couch MOND in some kind of mathematical metric because general relativity describes gravity geometrically as a curvature in a space-time metric. Both models introduce modifications to gravity that lead to extra degrees of freedom that play the role of dark matter.
While Newton's gravitational laws can be written as equations in vector form and can describe the gravitational field as a vector field, Einstein's general relativity is a metric tensor where a tensor field is added into Newton's gravitational dynamics. This metric tensor is a four-dimensional differentiable manifold called a Lorentzian manifold.
In these models, baryonic matter is treated as a perfect pressure-less fluid with an energy-momentum tensor. Perturbations introduced by additional vector and/or scalar fields can affect the energy-momentum tensor value, enhancing the impact of baryonic matter.
TeVeS introduces two extra fields to this manifold, a scalar field and a time-like vector field. At a background level, these fields modify the overall dynamics of gravity but they don't change the overall energy density of space-time. However, when a space-like perturbation is introduced, energy density is affected. Perturbations in the scalar field have negligible effects, but in the vector field they lead to growth. In other words, a vector field growing in space feeds into Einstein's equations and enhances both the gravitational potential and baryon density, an effect that mimics the effect of pressure-less dark matter. There are criticisms of this model, however. For example, a star operating under TeVeS gravity would be far too unstable to last billions of years without exploding. As well, some physicists challenge whether TeVeS can account for both galaxy rotation velocities and gravitational lensing. The latter problem can be solved by introducing a sterile neutrino with a mass of 11 eV. A hypothetical sterile neutrino possesses right-handed chirality. So far only left-handed neutrinos have been observed but right-handed ones are possible in the Standard Model, and all other fermions possess both kinds of chirality. The author of this referenced paper also discusses various ways that the validity of TeVeS could be tested.
MOG (modified gravity) developed by physicist John Moffat here in Canada, works differently. (I recommend checking this link on Wikipedia. His life story is an interesting one).
MOG introduces a very large tensor field that acts as a repulsive gravitational force that cancels the effect of gravity at smaller scales. In other words, it assumes the gravitational force is much higher than what we measure, but at scales starting at galaxy size and going smaller, its effects are increasingly diminished by the repulsive force introduced by the extra tensor field. This model introduces three scalar fields - the mass of and the strength of the introduced vector field are treated as scalar fields along with Newton's gravitational constant, which is preserved as a scalar field - into the space-time tensor metric that describes the dynamics of general relativity. That is why it's also called scalar-tensor-vector gravity. It describes all the observable effects of dark matter, including the CMB spectrum peak data. At scales smaller than galaxies (smaller than a few million solar masses), most of the gravitational force is canceled out by the repulsive force, predicting gravitational effects that coincide with general relativity. An excellent physics blog called Spinor Info, operated by Viktor T. Toth, discusses MOG and provides links to several current scientific papers that deal with it. I find it curious that this theory seems to have gotten little attention in the media, as its predictive power is very good and there are few observational inconsistencies with it. One way in which MOG's validity will shortly be tested is by refining the accuracy of the angular power CMB spectrum data. If you scroll back to that graph earlier in this article, you will notice there is a fair amount of uncertainty (the lengths of the multicoloured vertical bars) in these measurements particularly when you look at the third and later peaks. There is significant room for refinement there. Recall that dark matter is explained as a dampening of baryonic oscillations. That explanation is based on the standard cosmological model or Lambda cold dark matter theory. In MOG, these oscillations are explained by deepening the gravitational wells themselves. The current resolution of the data isn't good enough to prove which theory fits best, so neither is ruled out. As the resolution of galactic surveys improves, one or the other should win out.
Conclusion
The acid test for dark matter will be whether or not a cold dark matter candidate particle will be detected. The blueprint for a new particle physics project called the International Linear Collider was published in June this year (2013). Its main goal will be to hunt for dark matter particles. As the Large Hadron Collider finishes its current upgrade it too will be more than powerful enough to detect dark matter particles such as sneutrinos or neutralinos. If one of these particles is discovered, supersymmetry will also be right at the top of the headlines. If no candidate particles are found, research into gravity itself will likely be the new focus, with MOG being especially interesting to follow. The next few years in physics will be fascinating either way!