The Standard Model (SM) of particle physics is a theoretical framework of how particles of matter and energy interact, making the universe what it is. It is tremendously successful. It predicted the existence of W and Z bosons, the gluon, and top and charm quarks before any of these particles were ever detected in colliders. It also predicted the decay of the Z boson before it was confirmed at the Large Positron-Electron Collider at CERN. The Standard Model is not complete, however, because it does not describe the fundamental force of gravity nor does it describe dark energy or dark matter, both of which have been experimentally verified. It also suffers from an inherent problem called the hierarchy problem, which has to do with its inability to describe gravity in the language of quantum mechanics. Supersymmetry was proposed as a solution to this troubling problem, and it caught on, offering not only a hierarchy solution but also offering up some particle candidates for all the dark matter in the universe. However, supersymmetry stands in a no man's land where there is no shred of evidence to support it as a reality.
The previous article, Gauge Theory, goes into some detail about how the Standard Model was developed and describes some of the fundamental theories (such as gauge symmetry) that go into it. In this article, we go beyond the Standard Model by exploring the theory of supersymmetry.
Supersymmetry effectively doubles the number of the particles of the Standard Model, shown below. The question is why would we want to complicate matters? First, we should review what fundamental particles are.
What's a Particle?
Most of us recognize the familiar electron and perhaps the quarks that make up protons and neutrons in the nucleus of an atom. However, there are five other kinds of lepton particles here as well as force-carrying boson particles that we don't "see" in everyday life. The neutrinos are there all around us, streaming through us and through Earth as part of the Sun's solar wind but they are notoriously difficult to detect. They hardly ever interact with other matter particles - quarks and electrons - and they don't interact with the electromagnetic force. We can detect and measure the forces carried out by the gluon, photon and the W and Z bosons but they generally live as real particles only at very high energies. At everyday energies, physicists describe the force-carrying bosons as virtual particles. A virtual particle is a momentary excitation in a force field. These kinds of excitations are described by the perturbation theory in quantum field theory. In the last article, Gauge Theory, I described what a quantum field theory is and how it works as one of several theories embedded in the Standard Model. As an example of how virtual particles work, I'll take W and Z bosons, particles with a rest mass, as an example. These particles do not carry this mass as virtual particles, but they still conserve energy and momentum. The weak force interacts with all matter particles through the exchange of virtual W and Z bosons. However, "real" W and Z bosons, with mass (and energy) can be detected in the high-energy environment inside a collider. The photon is bit unusual because it exists as both a real particle and a virtual particle at everyday energy. For example, photons stream as "real" particles through air and the vacuum of space in the form of electromagnetic radiation such as radio waves. However, photons also exist at the radio antenna as virtual particles. Here, they are responsible for near field phenomena.
The longer a virtual particle exists the more it resembles a real particle, but virtual particles and real particles as separate entities is misleading. "Real particles" in quantum field theory, which underlies the Standard Model, are described just the same as virtual particles - as excitations (with various degrees of freedom) in underlying quantum fields. This is the mathematically consistent way to think of all particles.
Some particles live only in a very high-energy environment such as a particle collider, a cosmic ray interaction, or during the first few microseconds of the universe. These particles are unstable at everyday energy. They decay, often almost instantly, into smaller mass stable particles, often through complex chains of intermediate particles and even virtual particles along the way. These kinds of particle soups are pay dirt to physicists.
If you look again at the particle diagram above, you'll notice each particle's mass in the upper left corner in MeV/c2. This unit for mass (million electronvolts over the speed of light squared) hints at mass-energy equivalence, recalling Einstein's famous E = mc2. It also hints at how virtual and real particles can be equivalent mathematically. You will often see mass simply written as MeV and it is simply a convenient but technically incorrect shorthand. An eV (electron volt) is a unit of energy; an eV/c is a unit of momentum and an eV/c2 is a unit of mass. Generally, the more massive a particle is, the more energy it contains, but even the energy of massless particles such as photons can differ greatly. For example, a photon of green light has about 2.3 eV energy. X-ray photons have about 0.2 MeV (200,000 eV) of energy. A cosmic ray photon can have up to 1000 TeV (that's a whopping million million eV) of energy. Put a slightly different way than the statement above, particle energy often translates into particle mass, and the proton inside an atom's nucleus is a striking example of this. Up and down quarks, the quarks in ordinary matter have masses of just a few MeV/c2 each. However, a proton, made of three quarks, has a whopping mass of 938 MeV/c2. Why all this mass? A proton contains not only quarks but also gluons binding them together. As you can see, a gluon is a massless particle. However, gluons possess tremendous energy (it is quantum chromodynamics binding energy) and this energy really bumps up the proton's rest mass (again illustrating mass-energy equivalence).
The other four quarks - charm, strange, top and bottom - are much more massive (some are on the order of a billion eV each) than the up and down quarks inside atoms. In the Standard Model, elementary particles are organized into three families called generations, which differ by quantum number (flavour in the case of quarks and neutrinos) and mass, but their interactions are identical (top and bottom quarks still act like quarks for example).
Charm and strange quarks represent the second generation of quarks while top and bottom quarks represent the third generation. In a similar way, the muon is a second-generation lepton and a tau is a third generation lepton. We don't see second and third generation particles at everyday energy, however, because as soon as these higher mass particles are created they spontaneously decay into stable first generation up and down quarks and electrons, and they do so far too quickly to interact and combine into any "higher generation" protons, neutrons or atoms. Even when the universe was very young there was far too much energy for any of these higher generation particles to settle into atoms.
Neutrinos are an interesting exception to the generation rule. All three generations of neutrinos, matter particles of negligible mass that travel at the speed of light, are stable and they stream throughout the universe, spontaneously oscillating between all three flavours (generations).
I drew the graph below to get an idea of the range of SM particle masses. The differences in mass are so great I had to use a logarithmic scale. If we multiply mass by the speed of light squared, we get the energy equivalent of each mass. That is what we will mostly be looking at, as well as at energies around the TeV (1012 eV) level, when we explore supersymmetry particles. As you can see, none of these Standard Model particles quite approaches that energy/mass. The massive W and Z bosons are mapped out but the photon and gluon, both massless, are not shown, but they do have momentum and energy, as I mentioned. Observed photon energy ranges from about 10-15 eV (ultralow frequency radio waves) to 1021 eV (cosmic rays) but in theory a photon's wavelength can approach the infinitesimally small Planck length, which corresponds to an almost infinite energy. Gluon energy (taken as a normalized density) inside a baryon is in the 106 eV range.
No one knows why particles of matter come in three generations, and not one or two or four. The existence of fourth and higher generations of even more massive particles, though theoretically possible in the Standard Model, are considered to be very unlikely, based on experimental evidence from the LHC and the Tevatron colliders.
Do the force-carrying particles, the bosons, come in different generations? An interesting example is the Higgs boson. This particle comes into existence as the electroweak force breaks giving rise to the Higgs field, which imparts mass on particles. The Higgs boson isn't a force-carrying boson like the photon, gluon or the W and Z bosons because the Higgs field, though a gauge field like the electromagnetic, strong and weak forces, is a scalar field rather than a tensor field. It doesn't transfer energy and it can't accelerate particles. However, just like the gauge bosons, the Higgs boson is a quantum excitation (or perturbation) in a quantum field. Is there one Higgs boson or are there three, one corresponding to each generation of leptons and quarks? No one knows.
A similar question has been asked of the W and Z bosons of the weak force. Much heavier theoretical X and Y bosons could carry out the grand unified force (GUT). This fundamental force would consist of the electroweak and strong force combined into one force that would operate only at extremely high energy. As the universe cools, it breaks into the strong force and electroweak force. The EM force and the weak force at this point are still combined under yet another symmetry that will break when the universe cools further. This symmetry-breaking is mentioned in the previous article about Gauge Theory. X and Y bosons would be much more massive cousins of the W and Z bosons of the weak force, but whether these hypothetical bosons, or the Higgs boson, could be considered multi-generation particles is an open question.
Why leptons and quarks specifically come in three generations has led researchers to look for some connection between these two kinds of matter particle. Several researchers have been searching for hybrid particles called leptoquarks. These particles, part of several theories such as the GUT (SU(5) gauge symmetry theory, mentioned in the previous Gauge Theory article, come in three generations corresponding to those of the quarks and leptons, and they may carry information between quarks and leptons, allowing quarks and leptons to interact. Such an SU(5) symmetry particle is predicted to be astoundingly heavy, as massive as an atom of lead, and it would not feel the strong force as a separate force. This more fundamental particle would describe an even higher SU(5) symmetry. It would decay almost instantaneously, perhaps into a same-generation quark and lepton. Mass limits for these three generations of leptoquarks are not worked out and no potential leptoquarks have been detected.
The Standard Model diagram above does not include all known elementary particles. Each particle, both fermion (matter) and boson (force), in the Standard Model diagram has its own antiparticle, it's own antimatter twin in other words, owing to another kind of symmetry in the Standard Model, called charge-parity or CP symmetry. We call it antimatter but anti-force particles are included too. W+ and W- bosons are antiparticles of each other, and the Z boson, being neutrally charged, is its own antiparticle, much like the photon. Gluons are more complicated because they have colour charge. There are eight gluons based on colour charge and they transform under real representation. This is the mathematical way to saying gluons always exist in a kind of superimposed state, so you have to consider the gluons as an octet and this octet has its own antiparticle.
Physicist Paul Dirac predicted the existence of the positron, the antiparticle of the electron in the 1930's. Each particle's antiparticle twin has the same mass and lives at the same energy, so a positron is as stable as an electron and an anti charm quark is just as massive and unstable as a charm quark, for example. The difference is that the charge is reversed, so a positron is positively charged and an anti charm quark has an anti colour charge. Before supersymmetry ever came along, Dirac doubled the number of particles in the universe by using symmetry.
Below, hydrogen and antihydrogen atoms are compared. The "mirror" is CP symmetry. Antihydrogen, the simplest possible antimatter atom, has been produced in the lab. It is expected to have many if not all the same physical properties as hydrogen, even the same colour of glow when excited anti-atoms return to ground state.
Why don't we see antimatter planets and stars then? Every particle and its antiparticle immediately annihilate each other upon contact. The two atoms above would immediately explode into a mixture of gamma photons, neutrinos, electrons and positrons, so antihydrogen is held in a magnetic vacuum trap. This isn't a perfect symmetry; if it were, all matter and antimatter likely would have been annihilated long ago, and the universe would be empty of all matter. Instead, thanks to a mechanism called CP violation (a slightly imperfect symmetry favouring matter), a small excess of matter survived in the universe. Antimatter particles are produced naturally in beta decay and in cosmic rays as well as in colliders. Some neutral particles, such as photons, are their own antiparticle, and some particles are made up of both matter and antimatter. These are mesons. Unlike three-quark hadrons such as protons and neutrons in atomic nuclei, mesons are made up of two quarks, one of matter and another one of antimatter, a quark and antiquark held together by the strong force. There are many different kinds of mesons, depending on the type of quark and antiquark involved as well as their overall spin configuration. These quark pairs are all very unstable and they annihilate just as you would expect them to, but two quarks of different flavours decay a bit more slowly because they decay via weak interactions, changing flavour, first, suggesting that angular momentum (they spin around each other) keeps them around for a tiny moment before they annihilate.
As we've seen, the universe is already quite well stocked with various stable and unstable particles of force, anti-force, matter and antimatter. Why complicate it further?
Why Supersymmetry?
Supersymmetry, if it exists as a reality, doubles the number of particles in the Standard Model yet again. This operation is built on a symmetry between matter and force that would be apparent (unbroken) at very high energy. This unbroken supersymmetry space is called superspace. Superspace is impossible to visualize so there is no way around describing it mathematically. Hopefully what follows will give you a feel for this concept. Along with ordinary spatial dimensions, superspace also contains an equal number of dimensions that anticommute. A commutative operation is like putting on your socks - it doesn't matter what order you put them on, the end result is the same. A non-commutative operation is like putting on underwear and jeans, the order matters (hopefully). Anticommutative lives just in mathematics. Here, swapping the order of two functions negates the result altogether. Put according to Wolfram Mathworld, an operator * for which a * b = - b * a, is said to be anticommutative. Lie algebra, which underlies gauge theory, is an example of an anticommutative algebra.
Ordinary space dimensions correspond to bosonic degrees of freedom (can be swapped out) and anticommuting dimensions belong to fermionic degrees of freedom (can't be swapped out). You can get a hint of Pauli's exclusion principle here. You can describe superspace as a supermanifold that contains bosonic and fermionic coordinates, but these coordinates are not really sets of points but instead "dual points of view." When you transform the manifold in space-time you mix bosons and fermions. Okay, you can breathe again.
Each matter particle has a force superpartner and each force (boson - spin 0 or 1 or 2 in the case of the hypothetical graviton not included below) particle has a matter (fermion - spin 1/2) superpartner.
Supersymmetry or SUSY for short, was introduced in the1960's and developed in large part in the 1970's and 1980's.
It offers, in return for the complication of extra particles, a possible explanation for dark matter because any of its particles could be candidates for this mysterious mass that accounts for five times more matter than the ordinary matter physicists can account for. The luminous matter in the universe, stuff that can be detected such as gas, dust, planets and stars, doesn't explain the much higher than expected gravitational behaviour of the universe, such as too-high orbital rates of large-scale structures like galaxies. Particles such as neutrinos as well as non-radiating black holes, planets and brown dwarfs (all non-luminous) have been ruled out as insufficient in mass to account for it. The rest of the matter - undetectable by any currently known means - is called dark matter.
SUSY also offers an explanation for why the powers of the four fundamental forces differ so wildly from each other. In particular, the weak force is 10 quadrillion times more powerful than gravity. Why? This is the hierarchy problem, and it is pretty huge because ultimately by solving this problem SUSY offers a possible way to bridge the looming gap between quantum mechanics and general relativity, paving the way for an ultimate theory of all fundamental forces and particles - a theory of everything (TOE), a tall order to deliver! The Standard Model is based on three fundamental constants in nature - the gravitational constant, the speed of light and Planck's constant - to get fundamental units for length, time and mass. The problem comes in when using these constants to get a base unit for mass (Planck mass). It is many magnitudes too huge. It's far more massive than any of particles discovered so far. By introducing an extra symmetry to the Standard Model, this Planck-scale mass is cancelled out, bringing predicted masses for particles into line with what physicists measure in colliders. I will explore the hierarchy problem in more detail later on.
Third, supersymmetry offers help for something called gauge-coupling unification in the Standard Model. These three solutions will be explored in detail under "What Supersymmetry Does," later on.
In general, what SUSY does mathematically is that it reins in seemingly disparate forces and particles into a fairly neat and tidy higher symmetry, and symmetry, as we saw in Gauge Theory, seems to lie at the heart of particle physics.
How Supersymmetry Came To Be
Hironari Miyazawa first glimpsed the possibility of supersymmetry in 1966, when he tried unsuccessfully to find a relationship between baryons and mesons that involved an internal symmetry between the two groups of hadrons. Hadrons are quark-based composite particles. They come in baryon and meson form. Baryons, made up of three quarks, include the proton and the neutron. Mesons, which we explored a little earlier, are each made up of a quark and an antiquark, and unlike baryons, they are all extremely unstable.
In the1970's, supersymmetry was rediscovered as a new kind of structure that unifies all the fields in quantum field theory with space-time. In doing so, it also establishes a relationship between the different quantum natures of fermions and bosons. Fermions are all particles with a 1/2 quantum spin. These include electrons and other leptons as well as all quarks and any composite particle that contains an odd number of these particles, such as baryons. These particles, usually a part of matter, can only occupy one quantum state at a time thanks to the Pauli exclusion principle. Mathematically, they all obey the rules of Fermi-Dirac statistics. Bosons don't need to follow this rule. Any number of bosonic particles can all occupy the same quantum state at the same time. These particles have whole integer quantum spins and obey Bose-Einstein statistics. All the force carrier particles such as photons, W and Z bosons and gluons, as well as mesons (two half integer spins add up to an overall quantum spin of 1), are bosons, but even fermions of matter may display bosonic behaviour. For example, some materials, when cooled below a critical temperature transition into a state of superconductivity. Within these materials, electrons (that are not necessarily close together) form pairs called Cooper pairs, which act like bosons (two half integer spins add once again into a spin-1 "particle"). In a similar way, atomic nuclei of even mass number such as helium-4 can become (bosonic) superfluids. The mathematics of this rediscovered supersymmetry is based on a consistent Lie superalgebra structure, where the even elements of the algebra correspond to bosons and the odd elements correspond to fermions. This algebra already has "proof" from nature. It has been used successfully to model observed resonances inside atomic nuclei by relating bosonic and fermionic nuclear properties with each other.
This type of mathematics also closely links supersymmetry with string theory (more on this later on). Though discovered outside of string theory, Lie superalgebra was incorporated into string theory in the 1970's transforming it into superstring theory.
What Supersymmetry Is
Supersymmetry is a broken symmetry, at least at everyday energy. If it were an intact symmetry at "our" energy, particles and their superpartners would have the same mass and they would share the same interactions. An atom, for example would contain both electrons and selectrons (both having the same charge but one being fermionic and the other bosonic). Physics would be unrecognizable. However, when the universe was very young and very energetic, somewhere around the TeV scale of energy, supersymmetry was intact and both standard and SUSY particles would have existed. As the universe cooled, supersymmetry broke and SUSY particles decayed, leaving behind just one stable "fossil" particle, the lightest of the four neutralinos. The mechanism responsible for supersymmetry-breaking is not entirely worked out. There are currently three main theories, called gravity-mediated, gauge-mediated and anomaly-mediated SUSY-breaking.
Most symmetries in physics, such as the gauge symmetries mentioned in Gauge Theory, are created by fields that transform under tensor representations of space-time. Supersymmetry, on the other hand, is created by a transformation of space and time under a spinor representation. Remember the anticommuting coordinates I mentioned earlier? These are supersymmetry coordinates in ordinary space-time, and they come in the form of spinors. A spinor is unlike the spatial vectors and tensors we explored in Gauge Theory. Here, a 360-degree rotation transforms the numeric coordinates of a spinor* into their negatives, so it takes a 720-degree rotation to get back to the original coordinates. We have encountered a spinor before. In fact, spinors are incorporated into quantum mechanics to describe the 1/2-spins of all fermions. The quantum spin (which is not a physical rotation in space but is the intrinsic angular momentum) of the electron, for example, is a spinor in three dimensions. The spinor is essential to spin statistics theorem in quantum mechanics, Fermi-Dirac statistics and Bose-Einstein statistics, which say that bosonic fields commute and fermionic fields anticommute. This is the mathematical way of saying that two or more bosons can have the same quantum numbers but fermions can't. Combining the two fields gives you a single algebra, which along with a mathematical procedure called z2-grading to give even boson elements and odd fermion elements, is called a Lie superalgebra.
Lie algebras and Lie groups, introduced in the Gauge Theory article, describe gauge and other symmetries in the Standard Model, but they cannot introduce the kind of inversion that happens when fermions are swapped for bosons and vice versa. If the Lie algebra is graded, it becomes superalgebra, however, and it can describe these kinds of swaps. When this algebra is incorporated into the Standard Model, the number of particles is doubled. The simplest possible model based on this superalgebra is the Minimal Supersymmetric Standard Model (MSSM).
What Supersymmetry Does
For every particle there is a corresponding superpartner particle of higher mass. These higher masses indicate that supersymmetry is not an exact symmetry. Physicists knew even before starting with supersymmetry that it could not be exact because superparticles and regular SM particles would all have equal masses. The mathematics of supersymmetry, which solves the hierarchy problem, also puts the mass range for superparticles at the TeV scale, well above even top quark mass. For example, an electron has a superpartner selectron and a quark has a superpartner squark. Matter particles are given an "s" in front and force particles are given an "ino" at the end. Squarks and selectrons are bosons whereas quarks and electrons are fermions. Supersymmetry is expected to be intact down to around the TeV (1012 eV) scale of energy. This is about ten times the energy/mass of the top quark, which is believed to be about 173 GeV/c2, and the Higgs boson at about 125 GeV. This is the energy at which supersymmetry solves the hierarchy problem. Both the Large hadron Collider (LHC) and the Tevatron collider can achieve this energy. It is the energy at which physicists hope to find some of the lightest supersymmetric particles, such as neutralinos.
Supersymmetric particles are expected to be unstable with the exception of the lightest of four fermionic neutralino particles. The lightest neutralino is expected to be light enough to find in a high-energy collider.
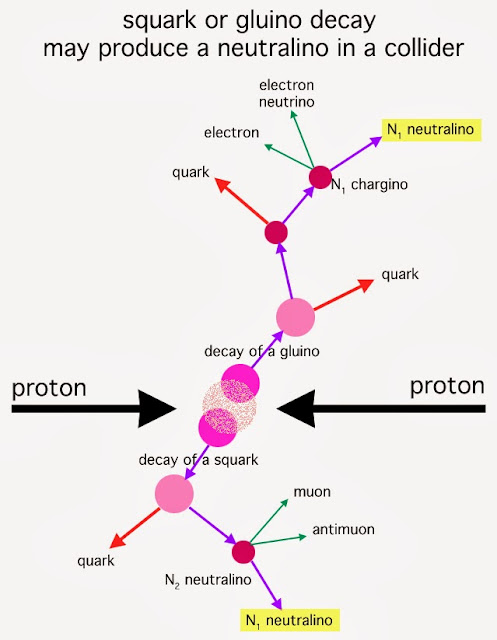
Like neutrinos these particles should interact only with the weak force and gravity, making them almost impossible to detect directly. However, when protons are smashed together (at the LHC) or protons are smashed with antiprotons (at the Tevatron collider), two other SUSY particles, squarks and gluinos, should be created at the energies produced by these collisions. These would decay before any possible signature is observable but their decay chains should leave behind one stable neutralino each, which leaves the detector unseen. Physicists know the total mass/energy before the collision, which is conserved, so all the mass/energy subtracted from all the decay products should come up just short. The diagram below shows two possible decays - gluino decay and squark decay, each of which produces one lightest (N1) neutralino.
In this way, physicists looking for the neutralino hope to find its missing energy signal. So far, even at close to 2 TeV energy, no missing mass has been detected. This should make any SUSY physicist feel a bit jittery, but this search is still in its early phase.
1) Dark Matter: Sneutrinos Versus Neutralinos
The boson superpartner of the neutrino is the sneutrino, so there should be sneutrinos, smuon sneutrinos and stau sneutrinos. These are all spin-0 superpartners of their fermion neutrinos, and they should be higher but fairly low mass because the neutrino itself is thought to have an infinitesimally small mass. A mixture of these three bosons is not a dark matter candidate because it would have been detected by now. The sneutrinos interact via Z boson exchange and this would have been detected. On the other hand, right-handed or sterile sneutrinos are possible. Having right-handed chirality, these particles would not interact with the Z-boson as strongly and may exist undetected.
More commonly, another superparticle, the neutralino, is mentioned in the physics literature as a dark matter candidate. This particle is a fermion like the neutrino and it is not a superpartner of it. The theory behind this particle is a little more involved. According to supersymmetry, each of the quantum fields for the photon, W and Z bosons, and the Higgs boson should include another quantum field representing a massive fermion - the photino (or bino), wino, zino (I know, they're terrible!) and Higgsinos, respectively. These were shown in the superparticle boson image earlier.
The bino and zino are neutral just like their SM particles. The winos are charged like the two W bosons. The Higgsinos are a weak isodoublet superpartner of the Higgs boson, with one part being charged and the other part being neutral.
The zino, bino and the neutral Higgsino all have the same quantum numbers (zero charge and quantum spin 1/2) so they can mix to form four mass eigenstates of the mass operator called "neutralino." Why four and not three? After electroweak symmetry breaking, the Higgsino becomes a pair of neutralinos and a single chargino.
A mass eigenstate is a free-particle solution to the wave equation of a particle or particles. An example of a mass eigenstate is an oscillating neutrino, which has electron, muon and tau oscillations, each of which should have a slightly different mass, but the mass eigenstate gives you a narrow range of possible mass bound by the heaviest tau component (0.5 eV, less than a millionth of an electron's mass) and the lightest electron component which could as low as zero-mass). There is no way to get exact values for the individual masses of the electron, muon and tau neutrino, because in nature the neutrino exists as an indeterminate quantum superposition of these three flavours.
In a similar operation, to get the neutralino mass eigenstate through electroweak symmetry breaking, physicists must take linear superpositions (a mixture) of the bino, wino, zino and Higgsinos.
I think of it this way: You put the wino, bino, zino and the Higgsinos into an "electroweak-breaking blender" and turn it on. After "blending," during which the electromagnetic force and the weak force emerge, you get four massive neutral fermions (neutralinos) and two charged massive fermions called charginos (X+ and X-). One chargino comes from the charged component of the Higgsino and the other one comes from the charged wino. The four neutralinos are four different mass eigenstates. These masses are most likely to be bino-like, wino-like, and Higgsino-like, but the mathematics allows the mixing to vary. The bino (photino)-like mass eignestate should be the lightest and the only stable neutralino.
This neutralino, called N1, is the particle of most interest to dark matter theorists, because it, being the lightest possible superparticle (LSP), shouldn't be able to decay into anything else. In our present low-energy universe, it can be thought of as a stable fossil of supersymmetry.
All heavier (all unstable) supersymmetric particles should ultimately decay into the N1 as well. A neutralino should have a mass in the range of 1 Tev and it should be able to interact with other particles through the weak force, much like a neutrino does. In many models the LSP can be created in the very young energetic universe and it, along with the lightest stable products of supersymmetric decay, can leave about the right amount of mass to fit the gravitational effects of dark matter. An answer neatly packaged and wrapped in a bow.
2) The Hierarchy Problem: A Possible Solution
The hierarchy problem in particle physics asks why the weak force is so much stronger, 1032 times, than gravity. This is a technical problem that is challenging to understand and it can be described in many different ways. In a nutshell, the hierarchy problem means that the real-life measurement of the power of the weak force doesn't agree with what the Standard Model calculation says - it's way too big. In order to make this calculation agree with experimental evidence, physicists must fine-tune (make quantum corrections to) the formula, without a known mechanism to explain why they have to do it, not a great place to be in terms of good theory. It's a fairly gangly part in an otherwise elegant model. The minimal supersymmetric theory (MSSM) was first proposed in 1981 to solve the hierarchy problem by stabilizing the weak scale of energy and this means stabilizing the Higgs boson mass, which is unstable when quantum corrections are done to it. The derivation of the mass of the Higgs boson's superpartner, the Higgsino, a fermion, lends its stability to the Higgs boson, and brings the weak force into line with experimental measurements.
One Way of Looking at the Hierarchy Problem
It starts with mass and the Planck units I mentioned earlier in this article. We've come across Planck units for length and time in past articles. Each of these units, described as smallest possible meaningful units, is incredibly tiny. Planck length is 10-35 m, about 1020 times smaller than an electron cloud, while Planck time is 10-44 seconds. Beyond these limits current physics no longer makes sense. Planck mass, however, just doesn't fit with these other units. It is huge, about 10-8 kg. That's about the mass of a flea, or 1023 times more massive than an electron. It is way out of whack with quantum-scale physics. The reason it's so big is that it is derived from Newtonian gravity and special relativity as well as quantum angular momentum. It takes the speed of light, the gravitational constant and the reduced Planck constant into its calculation. Planck mass is the mass of a Planck particle, which is a black hole whose radius is Planck length. Planck mass is thought to be an important number because at this mass, general relativity is as relevant to the physics of what's going on as quantum mechanics is - the two mutually exclusive theories try to meet up. We know that they must up meet somehow to explain what's happening to matter, space and time inside a black hole. Below Planck mass, only quantum mechanics describes the physics. Above Planck mass, only general relativity describes the physics.
In the 1970's, physicists realized that this problem has something to do with the Higgs field, which gives mass to particles. This is the field, carried out by the Higgs boson, which breaks the symmetry of the electroweak force. Unlike fermionic spinor fields and other bosonic gauge fields, the Higgs field is a scalar field, with the Higgs boson being a spin-0 scalar particle. This is the first scalar field discovered in nature. It differs from the vector and tensor fields of fermions and other bosons because it is independent of transformations on the field. The Higgs boson predicted by the Standard Model should have Planck mass and because it couples to all other particles of mass, they should have Planck-scale masses too. Obviously, we know that they don't. The mathematics in SUSY uses an extra symmetry that cancels all Planck-scale contributions to the mathematics and protects the Higgs field (and therefore mass) down to much lower realistic energies. Mathematically this is called Higgs quadratic mass renormalization. The quadratic divergence in the scalar self-energy of the Higgs field is cancelled.
Another Way of Looking at The Hierarchy Problem
When the universe was very young and very energetic, the Higgs field had an average (vacuum expectation value of zero. At this point, the W and Z bosons and the photon were all identical zero-mass particles. This field's energy jostled all over the place until the universe cooled to a certain temperature. According to quantum mechanics, even a perfect vacuum in space has a small but positive energy. This vacuum energy was very high when the universe was a tiny fraction of a second old, and it caused massive quantum fluctuations in the Higgs field, making it very unstable.
As the universe cooled, the Higgs field was locked into a particular non-zero positive energy of somewhere above 125 GeV, in a process that is a lot like a phase change such as water freezing into ice of a particular orientation or magnetic domains locking in place within cooling lava. This energy is calculated using the electroweak (SU(2) gauge theory part of the Standard Model mathematics. This value in turn sets the scale for all masses in the Standard Model. It gives the mass of the W boson at around 80 GeV, for example, and that mass has been experimentally verified in a collider. At very high energies, however, such as when the universe just came into existence and the electroweak force was still intact, the Standard Model no longer works. Here, there must be some modification to the Standard Model in order to describe physics at energies where gravity becomes as important as quantum mechanics (this is why the inside of a black hole is still a black box so to speak) and this is expected to happen at around Planck mass, where the corresponding energy is around 1019 GeV. At this energy, the Standard Model says the Higgs scalar boson itself should be Planck mass and we know that it isn't. It's at these high energies where the hierarchy problem with the Higgs scalar field becomes obvious. Below electroweak energy, there is no problem but at higher energy something must be in place to cancel out quadratic divergences (that's where this huge mass comes from) in the mathematics of quantum mechanics. The mathematics of supersymmetry does just that. To quote Oxford University's online article on SUSY, " - a boson-fermion symmetry gives the scalar masses 'protection' from quadratically divergent loop corrections by virtue of being related by symmetry to the fermion masses, which [themselves] are protected by chiral symmetry."
What is interesting here is that even at everyday energy, there is still significant vacuum energy fluctuation. This implies that the Higgs field in the our current universe is not entirely stable. The quantum mechanics in the Standard Model, however, say that the universe should be at its lowest energy state possible, in a minimum potential energy well in other words. The shape of this potential energy well can be determined by the scalar Higgs field. It means that the universe is at a local minimum energy, called a false vacuum, but not at its lowest possible energy (true vacuum). The graph below describes the energy of the Higgs scalar field Φ in a false vacuum. The universe exists where the dot is located, in a long-lived but slowly eroding metastable state. The universe's energy E is higher than in the true vacuum or ground state to the left of it.
 |
| User:Stannered;Wikipedia |
The hierarchy problem solution gives sypersymmetry great kudos but it does prove that supersymmetry is really a part of nature. There is also an alternative theory that stabilizes the Higgs field, called technicolor. Here, the Higgs boson is treated as an emergent particle of the strong (colour) force. The basic idea is that you repeat quantum chromodynamics (QCD) (this will hopefully be an article to come) at the Higgs electroweak energy scale. An additional stabilizing Higgs mechanism is produced by a new SU(6) gauge symmetry. There are still many technical problems with technicolor. This theory can accommodate the discovery of the Higgs boson, but it doesn't predict it.
3) Gauge Coupling Unification
The renormalization (fitting together) of the three gauge coupling constants - SU(1) the electromagnetic force photon, SU(2) the three weak force bosons, and SU(3) the eight strong force QCD gluons - isn't perfect in the Standard Model. It is sensitive to particle content and the present particle content of the model means that these three coupling constants don't quite meet up at a common energy scale, that of grand unification where the electromagnetic force and weak force (combined into the electroweak force) merge with the strong force at a particular energy. The incorporation of MSSM into the Standard Model allows the coupling constants to converge at one point, about 1016 GeV. Some physicists consider this feat to be indirect evidence for both MSSM and SUSY-based grand unification theories, but there are other (non-supersymmetry) mechanisms that can also do this job of convergence.
Where Does Supersymmetry Stand?
1) Where are the SUSY particles?
No supersymmetric particles have been discovered even by smashing protons apart at an energy approaching 8 TeV in the LHC. This energy is divided among various quarks and gluons that make up each proton, which means a new particle of at least 1 TeV could be produced in the mixture of broken proton parts. The lightest theoretical SUSY particles should be right in this range and not much higher. This limit is ironically thanks to the recent Higgs boson discovery (as I write this, physicists are receiving the Nobel prize in physics for it). The Standard Model puts the Higgs mass at the huge Planck mass but supersymmetry brings its predicted mass right down to around 125 GeV, right where it was discovered to be. All particles of mass must interact with the Higgs boson via the Higgs field, and this interaction puts an upper limit on the masses of all the superparticles. If none are found at this energy, supersymmetry, at least in its present simplest form, must not valid. Having to add corrections to the SUSY mechanism to account for a higher superparticle mass scale would seem to take the lustre off what was once its best quality - simplification of the Standard Model.
The LHC collider hasn't been running at this energy for long so there is still hope to see these elusive particles. It may also be possible to build entirely new theories, which still retain some SUSY components while accommodating slightly higher masses.
2) The Strange B-Meson: End of SUSY?
Even so, it is hard not to think of supersymmetry as a theory on life support, and recent collider strange B-meson data seems to spell its demise even more direly.
A collider is built like a pipe that accelerates particles such as protons to close to the speed of light, shooting them straight at each other. Built around the pipe, where the collision occurs, are massive sensitive detectors that look like super thick insulation. These detectors pick up a tremendous amount of data about where every single particle goes and there are many, many possible particles each with momentum and a trajectory. It requires an enormous amount of computer processing to recreate a single collision. To make matters more challenging, some collision results are extremely rare occurrences, so millions of collisions may be required in order to get significant data. There is sometimes only a very small probability that a particular decay chain will occur and particles specific to that decay will reveal themselves. An example of this is strange B meson decay. The strange B meson, (predicted by the Standard Model) is of great interest to physicists. It undergoes spooky oscillations and its very occasional decay into two particles called muons gave researchers direct evidence for CP violation. When two protons collide, the strange B meson itself shows up only occasionally, and when it does, it only very rarely decays into two muon particles (μ + and μ -).
The Standard Model predicts it will decay into muon particles only once every 280 million times. What makes this occurrence so rare is that this decay depends on the fleeting appearance of certain virtual particles during the collision. The results of the LHC closely match this prediction, at once every 310 million times. Supersymmetry predicts a far higher rate, by a factor of about 100, because superparticles should also be present, influencing the decay. This delivers a blow to supersymmetry's credibility. But it may not be as fatal as some physicists claim because the error margin in the statistical agreement between the observed rate and the predicted SM rate is quite large (though acceptable), and also because in the most stripped down version of SUSY (with the fewest number of particle couplings), strange B meson - muon decay is suppressed enough to agree with experimental results. The LHC, the only collider with enough energy to produce strange B mesons, is now undergoing an upgrade so that it can run at up to 13 TeV. Hopefully then, strange B meson data and the presence or absence of the N1 neutralino will either prove or disprove SUSY. In the meantime, there is a real edge-of-the-seat feeling waiting for what kind physics is hiding around the corner.
Supersymmetry Hints at String Theory
Supersymmetry was incorporated into another particle theory called string theory in the 1970's. String theory at that time described only bosons. Incorporating the mathematics of supersymmetry allowed for the inclusion of fermions as well. Supersymmetry also performs a feat reminiscent of the hierarchy solution by canceling out certain terms and therefore simplifying string theory equations. Without supersymmetry, string theory contains awkward inconsistencies like infinite values and imaginary energy levels. Unlike supersymmetry, string theory by its nature operates up to the Planck scale, making particle "strings" far too tiny to directly detect. However, superparticles fit comfortably into string theory. Here, the breaking of supersymmetry (as well as other symmetries) can be modeled as higher-energy strings losing energy and transforming into strings with lower energy vibrations. If a superparticle is eventually detected, it would lend proof not only for supersymmetry but offer tremendous support for string theory as well. Perhaps string theory's best attribution is that it easily lends a theoretical framework for quantum gravity by combining quantum field theory with general relativity. Doing so introduces a massless spin-2 string called the graviton.
While the charm of string theory is obvious even to laypeople like myself, like supersymmetry, there needs to be some evidence to back it up, such as the discovery of a superparticle or some evidence for the extra dimensions that string theory specifies. Two mathematically beautiful theories - supersymmetry and string theory - are now at the mercy of what the LHC will find which it comes back online.
What is certain is that some kind of "new physics," physics that goes beyond the Standard Model, MUST exist somehow, waiting in the wings.
*ASIDE: These concepts are not even close to easy for most of us. There is just no way to visualize a spinor, for example. When reading about gauge theory, I could sort of visualize how three-dimensional space is built up from a grid of three-dimensional vectors or even tensors, but not from spinors. I could also faintly grasp in my imagination how this grid transforms at least in three spatial dimensions, but there is no way to do that with a spinor grid or matrix. However, the mathematics describes precisely what's going on. The spinor transformation is just a very simple example of how mathematics takes our understanding to unfathomable places, places that are actually impossible in our everyday three-dimensional world. It's a little bit terrifying letting go of intuition and allowing math to take the reigns. I hope that you have felt this thrilling spark of wonder as well. To paraphrase Galileo's famous statement, if God has written the poetry of this universe, it must certainly be written in the language of math.






No comments:
Post a Comment
Note: Only a member of this blog may post a comment.